本系列文章是根据Shapely官方文档翻译整理,学习任何一个Python第三方库,其官方文档都是最好的学习资料。相比网络搜索得到的一些资料,官方文档是权威的一手资料,其内容全面、准确可靠。通过官方文档入手,能够保证学习认知不会有大偏差。在学习完官方文档后,可以在寻找其他资料进一步学习。
点击“阅读原文”或者直接访问下方链接,查看翻译整理的“Shapely 2.0.0 中文文档”。
https://www.mizhushare.com/docs/shapely-2-0-0-%e4%b8%ad%e6%96%87%e6%96%87%e6%a1%a3/-
可以通过百度网盘获取,需要在本地配置代码运行环境:
链接:https://pan.baidu.com/s/1iWGGhB4kra9V7bUj-CWR0w?pwd=mnsj提取码:mnsj
-
前往GitHub详情页面,单击 code 按钮,选择Download ZIP选项:
https://github.com/returu/Shapelyshapely.affinity模块中有一组仿射变换函数,它们通过直接向仿射变换矩阵提供系数,或使用特定的、命名的变换(旋转、缩放等)来返回变换后的几何要素。这些函数可以用于所有的几何要素类型(GeometryCollection除外),而3D类型要么被保留,要么被3D仿射变换所支持。-
shapely.affinity.affine_transform(geom, matrix):
返回一个使用仿射变换矩阵变换后的几何对象。
系数矩阵以列表或元组的形式提供,对于二维或三维变换,分别有6或12项。
对于二维仿射变换,6个参数矩阵为:[a, b, d, e, xoff, yoff]。
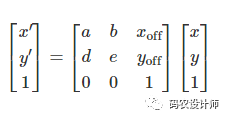
转换后的坐标方程如下所示:
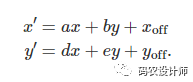
对于三维仿射变换,12个参数矩阵为:[a, b, c, d, e, f, g, h, i, xoff, yoff, zoff]。
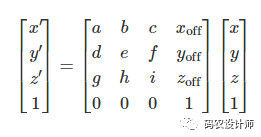
转换后的坐标方程如下所示:
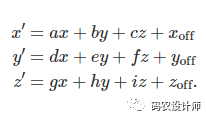
-
shapely.affinity.rotate():
1shapely.affinity.rotate(geom,
2 angle,
3 origin=’center’,
4 use_radians=False)
返回一个二维平面上的旋转几何对象。
旋转的角度可以通过设置use_radians=True来指定度数(默认)或弧度。正的角度是逆时针旋转,负的是顺时针旋转。
旋转原点可以是一个关键字’center’(表示中心)(默认),’centroid’(表示质心),一个点对象或一个坐标元组(x0, y0)。
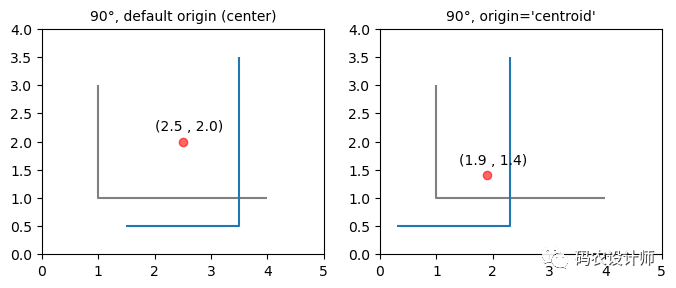
使用不同的旋转原点,将LineString(灰色)逆时针旋转90°(蓝色):
1>>> line = LineString([(1, 3), (1, 1), (4, 1)])
2>>> line
3<LINESTRING (1 3, 1 1, 4 1)>
4
5# 使用center作为旋转原点,逆时针旋转90°
6>>> roated_a = affinity.rotate(line , 90)
7>>> roated_a
8<LINESTRING (1.5 0.5, 3.5 0.5, 3.5 3.5)>
9
10# 使用centroid作为旋转原点,逆时针旋转90°
11>>> roated_b = affinity.rotate(line , 90 , origin="centroid")
12>>> roated_b
13<LINESTRING (0.3 0.5, 2.3 0.5, 2.3 3.5)>
结果如下图所示:
-
shapely.affinity.scale():
1shapely.affinity.scale(geom,
2 xfact=1.0,
3 yfact=1.0,
4 zfact=1.0,
5 origin=’center’)
返回一个按比例缩放的几何对象,沿每个维度都有相应的缩放系数。负的比例系数将对坐标进行镜像操作。
缩放原点可以是一个关键字’center’(表示中心)(默认),’centroid’(表示质心),一个点对象或一个坐标元组(x0, y0)。
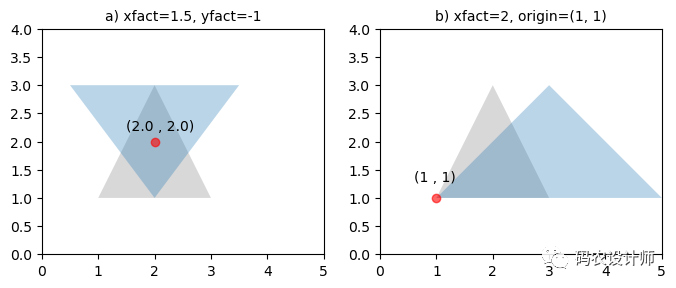
例如,对一个三角形几何对象执行缩放操作:
1>>> triangle = Polygon([(1, 1), (2, 3), (3, 1)])
2>>> triangle
3<POLYGON ((1 1, 2 3, 3 1, 1 1))>
4
5# 沿x方向放大1.5倍,并在y轴上进行镜像
6>>> triangle_a = affinity.scale(triangle, xfact=1.5, yfact=-1)
7>>> triangle_a
8<POLYGON ((0.5 3, 2 1, 3.5 3, 0.5 3))>
9
10# 沿x方向放大2倍,自定义原点在(1,1)
11>>> triangle_b = affinity.scale(triangle, xfact=2, origin=(1,1))
12>>> triangle_b
13<POLYGON ((1 1, 3 3, 5 1, 1 1))>
结果如下图所示(灰色为原始三角形,蓝色为结果三角形):
b)沿x方向放大2倍,自定义原点在(1,1)。
-
shapely.affinity.skew():
1shapely.affinity.skew(geom,
2 xs=0.0,
3 ys=0.0,
4 origin=’center’,
5 use_radians=False)
返回一个沿x和y维度设定的角度进行扭曲操作的几何对象。
扭曲角度可以用度数(默认)或者通过设置use_radians=True来指定弧度。
扭曲原点可以是一个关键字’center’(表示中心)(默认),’centroid’(表示质心),一个点对象或一个坐标元组(x0, y0)。
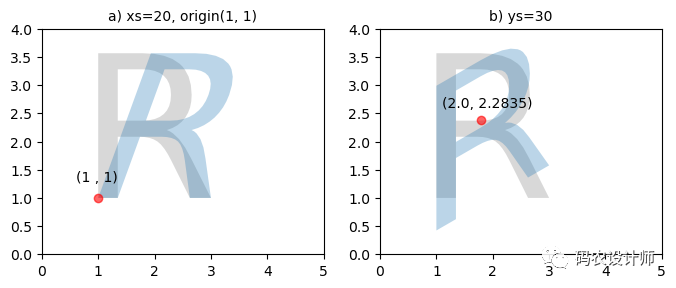
例如,对一个R形几何对象执行扭曲操作:
1>>> from shapely.wkt import loads as load_wkt
2
3# 读取数据,生成R形几何对象
4>>> R = load_wkt('''
5... POLYGON((2.218 2.204, 2.273 2.18, 2.328 2.144, 2.435 2.042, 2.541 1.895,
6... 2.647 1.702, 3 1, 2.626 1, 2.298 1.659, 2.235 1.777, 2.173 1.873,
7... 2.112 1.948, 2.051 2.001, 1.986 2.038, 1.91 2.064, 1.823 2.08, 1.726 2.085,
8... 1.347 2.085, 1.347 1, 1 1, 1 3.567, 1.784 3.567, 1.99 3.556, 2.168 3.521,
9... 2.319 3.464, 2.441 3.383, 2.492 3.334, 2.536 3.279, 2.604 3.152,
10... 2.644 3.002, 2.658 2.828, 2.651 2.712, 2.63 2.606, 2.594 2.51, 2.545 2.425,
11... 2.482 2.352, 2.407 2.29, 2.319 2.241, 2.218 2.204),
12... (1.347 3.282, 1.347 2.371, 1.784 2.371, 1.902 2.378, 2.004 2.4, 2.091 2.436,
13... 2.163 2.487, 2.219 2.552, 2.259 2.63, 2.283 2.722, 2.291 2.828, 2.283 2.933,
14... 2.259 3.025, 2.219 3.103, 2.163 3.167, 2.091 3.217, 2.004 3.253, 1.902 3.275,
15... 1.784 3.282, 1.347 3.282))''')
16>>> R
17<POLYGON ((2.218 2.204, 2.273 2.18, 2.328 2.144, 2.435 2.042, 2.541 1.895, 2...>
18
19# 沿X方向的扭曲角度为20°,原点在(1,1)
20>>> skew_a = affinity.skew(R , xs=20 , origin=(1,1))
21>>> skew_a
22<POLYGON ((2.656 2.204, 2.702 2.18, 2.744 2.144, 2.814 2.042, 2.867 1.895, 2...>
23
24# 沿Y方向的扭曲角度为30°,使用默认原点
25>>> skew_b = affinity.skew(R , ys=30)
26>>> skew_b
27<POLYGON ((2.218 2.33, 2.273 2.338, 2.328 2.333, 2.435 2.293, 2.541 2.207, 2...>
结果如下图所示(灰色为原始三角形,蓝色为结果三角形):
b)沿Y方向的扭曲角度为30°,使用默认原点。
-
shapely.affinity.translate():
1shapely.affinity.translate(geom,
2 xoff=0.0,
3 yoff=0.0,
4 zoff=0.0)
返回一个沿各维度平移的几何对象。
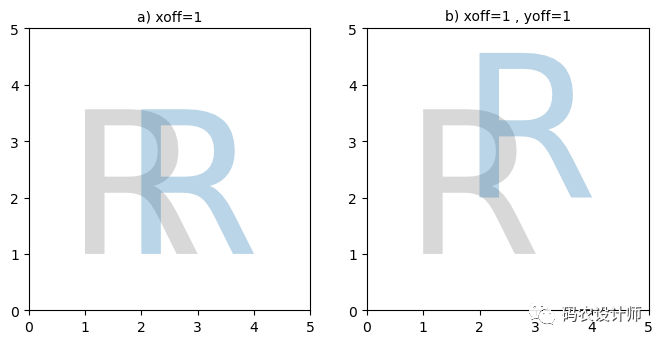
例如,对上面生成的R形几何对象执行平移操作:
1>>> R
2<POLYGON ((2.218 2.204, 2.273 2.18, 2.328 2.144, 2.435 2.042, 2.541 1.895, 2...>
3
4# 沿X方向平移1
5>>> translate_a = affinity.translate(R , xoff = 1)
6>>> translate_a
7<POLYGON ((3.218 2.204, 3.273 2.18, 3.328 2.144, 3.435 2.042, 3.541 1.895, 3...>
8
9# 沿X和Y方向各平移1
10>>> translate_b = affinity.translate(R , xoff = 1 , yoff =1)
11>>> translate_b
12<POLYGON ((3.218 3.204, 3.273 3.18, 3.328 3.144, 3.435 3.042, 3.541 2.895, 3...>
结果如下图所示(灰色为原始三角形,蓝色为结果三角形):
b)沿X和Y方向各平移1。

END

本篇文章来源于微信公众号: 码农设计师
