本系列文章配套代码获取有以下两种途径:
-
通过百度网盘获取:
链接:https://pan.baidu.com/s/1XuxKa9_G00NznvSK0cr5qw?pwd=mnsj提取码:mnsj
-
前往GitHub获取:
https://github.com/returu/PyTorch参数估计:
-
均方误差:
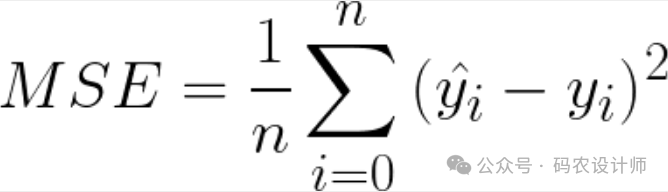

-
梯度下降算法:
-
初始化参数:初始化模型的参数,这些参数通常是随机初始化的; -
计算损失函数:该函数通常表示预测值与真实值之间的差异; -
计算梯度:计算损失函数关于模型参数的梯度,这个梯度指示了参数应该调整的方向; -
更新参数:根据计算出的梯度,按照一定的学习率来更新模型参数。学习率控制了每次更新的幅度,如果学习率过大,可能会导致算法不收敛;如果学习率过小,则可能会导致算法收敛速度过慢; -
重复迭代:重复执行步骤2-4,直到达到某个停止条件,例如梯度向量的幅值接近0,或者损失函数的变化小于某个阈值,或者达到预设的最大迭代次数。
实现线性回归:
-
1、生成并可视化数据:
# 设置随机数种子,保证运行结果一致
torch.manual_seed(2024)
def get_fake_data(num):
"""
生成随机数据,y = 0.5 * x +30并加上一些随机噪声
"""
x = torch.randint(low = -5, high=30, size=(num,)).to(dtype=torch.float32)
y = 0.5 * x +30 + torch.randn(num,)
return x,y
x , y = get_fake_data(num=11)
# 可视化数据
fig = plt.figure()
plt.plot(x , y , 'o')
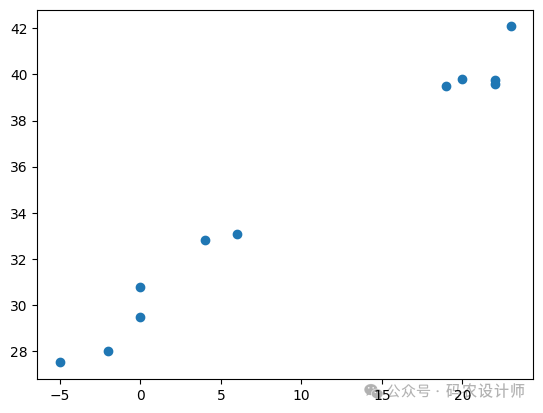
-
2、定义梯度函数:
# 定义模型:
def model(x , w , b):
return w * x + b
# 定义损失函数:
def loss_fn(y_p , y):
squared_diffs = (y_p - y)**2
return squared_diffs.mean()
# 计算导数:
def dloss_fn(y_p , y):
dsq_diffs = 2*(y_p - y)/y_p.shape[0]
return dsq_diffs
def dmodel_dw(x ,w ,b):
return x
def dmodel_db(x , w , b):
return 1.0
# 返回关于w和b的损失梯度的函数:链式法则
def grad_fn(x , y , y_p , w , b):
dloss_dtp = dloss_fn(y_p , y)
dloss_dw = dloss_dtp * dmodel_dw(x ,w ,b)
dloss_db = dloss_dtp * dmodel_db(x ,w ,b)
return torch.stack([dloss_dw.sum() , dloss_db.sum()])
-
3、求解参数值:
# 初始化参数:
w = torch.ones(())
b = torch.zeros(())
# 循环训练:
def training_loop(n_epochs , learning_rate , params , x , y):
for epoch in range(1 , n_epochs+1):
w,b = params
y_p = model(x,w,b)
loss = loss_fn(y_p ,y)
grad = grad_fn(x , y , y_p , w , b)
params = params -learning_rate*grad
if epoch % 10 ==0:
print(f"Epoch : {epoch} , Loss : {loss}")
print(f"Params : {params} , Grad : {grad}")
print("-----")
return params
training_loop(n_epochs=500 , learning_rate=0.02 , params=torch.tensor([1.0 , 0.0]) , x=x , y=y)
Epoch :10 , Loss :9.902059470433812e+17
Params : tensor([-5.1232e+08, -2.3935e+07]) , Grad : tensor([2.9021e+10, 1.3558e+09])
-----
Epoch :20 , Loss :3.3471030602793666e+35
Params : tensor([-2.9786e+17, -1.3916e+16]) , Grad : tensor([1.6873e+19, 7.8827e+17])
-----
Epoch :30 , Loss : inf
Params : tensor([-1.7318e+26, -8.0907e+24]) , Grad : tensor([9.8097e+27, 4.5830e+26])
-----
Epoch :40 , Loss : inf
Params : tensor([-1.0068e+35, -4.7039e+33]) , Grad : tensor([5.7033e+36, 2.6645e+35])
-----
Epoch :50 , Loss : nan
Params : tensor([nan, nan]) , Grad : tensor([nan, nan])
。。。。。。
。。。。。。
-
4、改进模型:
training_loop(n_epochs=5000 , learning_rate=1e-4 , params=torch.tensor([1.0 , 0.0]) , x=x , y=y)
training_loop(n_epochs=1000 , learning_rate=1e-2 , params=torch.tensor([1.0 , 0.0]) , x=x*0.1 , y=y)
-
5、可视化迭代效果:
from IPython import display
def training_loop(n_epochs , learning_rate , params , x , y):
for epoch in range(1 , n_epochs+1):
w,b = params
y_p = model(x,w,b)
loss = loss_fn(y_p ,y)
grad = grad_fn(x , y , y_p , w , b)
params = params -learning_rate*grad
if epoch % 100 ==0:
display.clear_output(wait=True)
plt.plot(x , y_p)
plt.plot(x , y , 'o')
# 获取xy轴的范围
xmin,xmax,ymin,ymax = plt.axis()
plt.text(x=xmax*0.2,
y=ymax*0.9,
s=f"{w*0.1:.3f}x+{b:.3f}")
plt.show()
plt.pause(0.5)
return params
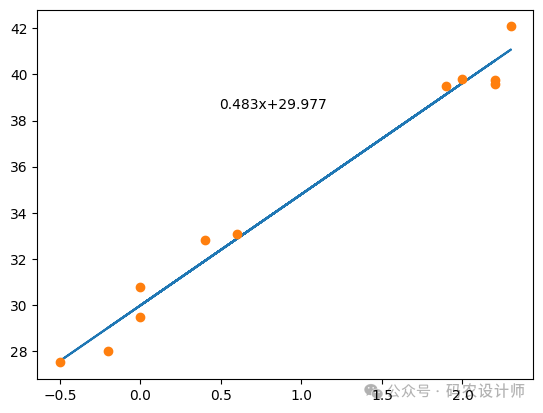
更多内容可以前往官网查看:
https://pytorch.org/


本篇文章来源于微信公众号: 码农设计师
