本系列文章配套代码获取有以下两种途径:
-
通过百度网盘获取:
链接:https://pan.baidu.com/s/1XuxKa9_G00NznvSK0cr5qw?pwd=mnsj提取码:mnsj
-
前往GitHub获取:
https://github.com/returu/PyTorch自动求导:
-
张量(Tensor):PyTorch 中的所有数据都是通过张量来表示的。除了存储数据外,张量还知道如何从其创建的操作中计算梯度。要使张量能够跟踪其历史操作和计算梯度,需要在创建时设置 requires_grad=True。 -
前向传播(Forward):在模型的前向传播过程中,输入数据经过模型得到输出。此时,PyTorch 会跟踪和构建用于计算输出的操作的计算图。 -
反向传播(Backward):在得到输出和相应的损失后,可以使用 backward() 方法进行反向传播。此时,PyTorch 会根据计算图使用链式法则自动计算每个参数的梯度,并累积到 grad 属性中。 -
优化器(Optimizer):一旦得到了梯度,就可以使用优化器(如 SGD、Adam 等)来更新模型的参数。优化器会根据计算出的梯度来调整模型参数,以最小化损失函数。该部分内容后续会介绍。 -
梯度清零(Gradient Zeroing):在每次迭代开始时,通常需要清零参数的梯度,否则新的梯度会累加到之前的梯度上。这可以通过调用 grad.zero_() 方法或使用优化器的 zero_grad() 方法来实现。
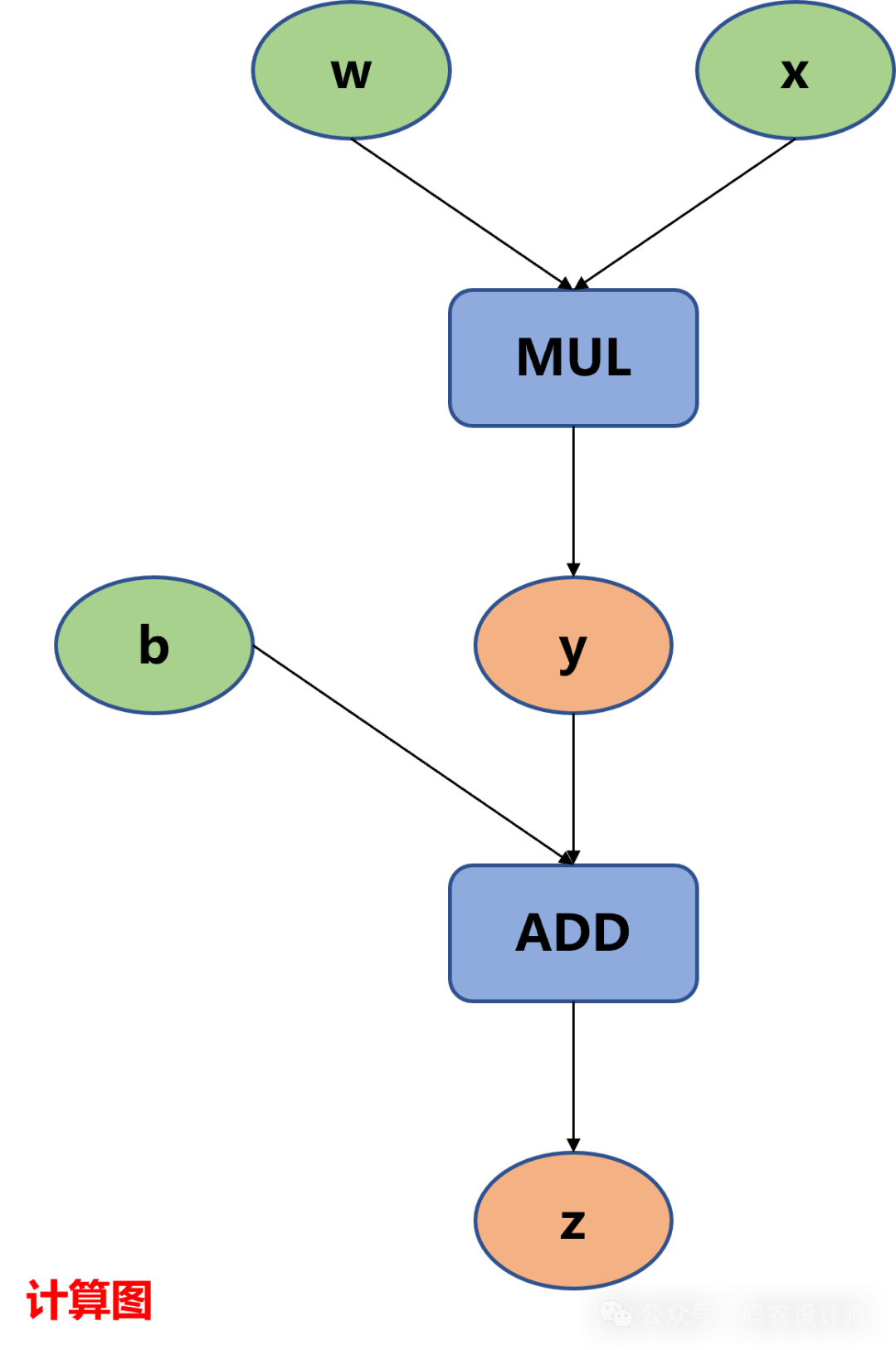
计算图:
>>> x = torch.ones(1)
>>> w = torch.rand(1 , requires_grad=True)
>>> b = torch.rand(1 , requires_grad=True)
>>> y = w * x
>>> z = y + b
# 查看变量的requires_grad属性
>>> x.requires_grad , w.requires_grad , b.requires_grad
(False, True, True)
# 虽然没有指定y和z需要求导,但是两者依赖于w和b,因此y和z的requires_grad属性会被自动设置为True
>>> y.requires_grad , z.requires_grad
(True, True)
-
叶子节点(Leaf Tensor):当Tensor的requires_grad=False时,即为叶子节点;当Tensor的requires_grad=True时,并且是由用户直接创建时,也为为叶子节点。通常为输入数据或模型参数。叶子节点没有从其他节点接收梯度的概念,因为它们是计算图的起点。 -
非叶子节点:这些节点是由操作产生的,它们的值取决于其输入节点。非叶子节点会接收来自其上游节点的梯度,并可能在反向传播过程中将其传递给下游节点。通常情况下,不会使用非叶子节点的梯度信息,这样可以节省内存/显存。
# 查看是否为叶子节点
>>> x.is_leaf , w.is_leaf , b.is_leaf
(True, True, True)
>>> y.is_leaf , z.is_leaf
(False, False)
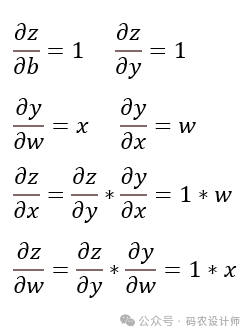
-
grad_fn 属性引用了创建该张量的 Function 对象,这个对象类型通常是 PyTorch 自动求导系统内部使用的类型之一,用于在反向传播过程中计算梯度。 -
next_functions 是 grad_fn 对象的一个属性,它返回一个包含元组的列表,这些元组包含了创建当前 tensor 的输入张量及其对应的 Function 对象,即它提供了对计算图中上一层的引用。
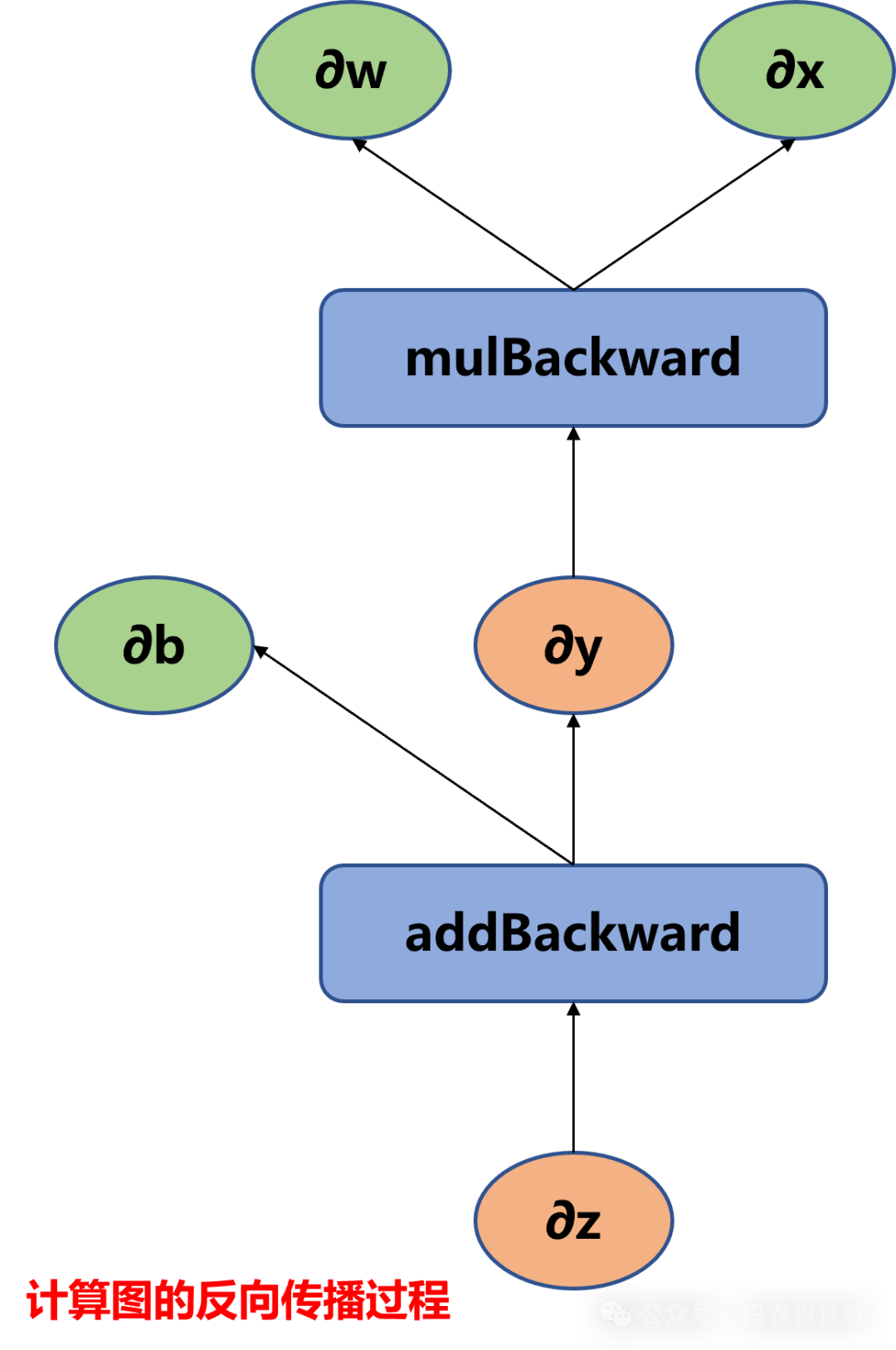
# 查看Tensor z的反向传播函数
# z是add函数的输出,因此它的反向传播函数为AddBackward
>>> z.grad_fn
<AddBackward0 object at 0x000001FDC4914700>
# 叶子节点的grad_fn属性属性为None
>>> x.grad_fn , w.grad_fn , b.grad_fn
(None, None, None)
# next_functions属性保存了grad_fn的输入,为一个tuple
# z = y + b
# 第一个是y,其是mul函数的输出,因此其反向传播函数为MulBackward
# 第二个是b,它是叶子节点(grad_fn属性属性为None),需要求导(梯度是累加的AccumulateGrad)
>>> z.grad_fn.next_functions
((<MulBackward0 object at 0x000001FDC4914700>, 0), (<AccumulateGrad object at 0x000001FDC48C6CD0>, 0))
# 查看Tensor y的反向传播函数
# y是mul函数的输出,因此它的反向传播函数为MulBackward
>>> y.grad_fn
<MulBackward0 object at 0x000001FDC4914700>
# y = w * x
# 第一个是w,它是叶子节点(grad_fn属性属性为None),需要求导(梯度是累加的AccumulateGrad)
# 第二个是x,它是叶子节点(grad_fn属性属性为None),不需要求导(梯度为None)
>>> y.grad_fn.next_functions
((<AccumulateGrad object at 0x000001FDC48C6CD0>, 0), (None, 0))
反向传播:
torch.autograd.backward(tensors,
grad_tensors=None,
retain_graph=None,
create_graph=False)
-
tensors:用于计算梯度的张量。torch.autograd.backward(y)等价于y.backward(); -
grad_tensors:与tensors相同大小的张量或张量列表,用于指定每个tensors的梯度。对于y.backward(),grad_tensors相当于链式法则∂z/∂x=∂z/∂y∗∂y/∂x中的∂z/∂y; -
retain_graph:反向传播需要缓存一些中间结果,在反向传播之后,缓存会被清除。可以将其设置为True来保留中间结果以便之后再次使用,用来进行多次反向传播;
-
create_graph:控制反向传播过程是否再次构建计算图。如果设置为True,则梯度计算本身将构成一个图,这样就可以计算高阶导数。
需要注意的是,调用backward()将导致导数在叶子节点上累加,即每个叶子节点的梯度将在上一次迭代中计算的梯度之上累加。之所以这样设计,是为了在复杂模型中使用梯度提供更多的灵活性和控制力。为了防止这种情况发生,需要在每次迭代时使用zero_()方法将梯度归零。
# 反向传播
# 为了能够进行多次反向传播,需要指定retain_graph=True来保存不需要更新的值(x)
>>> z.backward(retain_graph=True)
# 计算梯度
>>> w.grad , b.grad
(tensor([1.]), tensor([1.]))
# 再次反向传播
>>> z.backward(retain_graph=True)
# 多次反向传播,梯度累加
>>> w.grad , b.grad
(tensor([2.]), tensor([2.]))
# 在反向传播前将w的梯度清零
>>> w.grad.zero_()
tensor([0.])
# 再次反向传播
>>> z.backward()
# b的梯度仍是累加的
>>> w.grad , b.grad
(tensor([1.]), tensor([3.]))
利用自动求导实现线性回归:
-
生成数据:
# 设置随机数种子,保证运行结果一致
torch.manual_seed(2024)
def get_fake_data(num):
"""
生成随机数据,y = 0.5 * x +30并加上一些随机噪声
"""
x = torch.randint(low = -5, high=30, size=(num,)).to(dtype=torch.float32)
y = 0.5 * x +30 + torch.randn(num,)
return x,y
x , y = get_fake_data(num=11)
# 对输入数据做归一化处理
x_new = x * 0.1
-
定义函数:
# 定义模型:
def model(x , w , b):
return w * x + b
# 定义损失函数:
def loss_fn(y_p , y):
squared_diffs = (y_p - y)**2
return squared_diffs.mean()
-
循环训练,求解参数值:
>>> x = torch.ones(1)
>>> w = torch.rand(1 , requires_grad=True)
>>> b = torch.rand(1 , requires_grad=True)
>>> y = w * x + b
# tensor.data仍是一个tensor
>>> w.data
tensor([0.3697])
# requires_grad属性为False,说明其已经独立于计算图了
>>> w.data.requires_grad
False
def training_loop(n_epochs , learning_rate , params , x , y):
for epoch in range(1 , n_epochs+1):
#前向传播
y_p = model(x,*params)
loss = loss_fn(y_p ,y)
# 反向传播:自动计算梯度
loss.backward()
# 更新参数
params.data -= learning_rate * params.grad.data
if epoch % 10 ==0:
print(f"Epoch : {epoch} , Loss : {loss}")
print(f"Params : {params} , Grad : {params.grad}")
print("-----")
# 梯度清零
params.grad.zero_()
return params
training_loop(n_epochs=1000 , learning_rate=1e-2 , params=torch.tensor([1.0 , 0.0],requires_grad=True) , x=x_new , y=y)
更多内容可以前往官网查看:
https://pytorch.org/


本篇文章来源于微信公众号: 码农设计师
