本系列文章配套代码获取有以下两种途径:
-
通过百度网盘获取:
链接:https://pan.baidu.com/s/1XuxKa9_G00NznvSK0cr5qw?pwd=mnsj提取码:mnsj
-
前往GitHub获取:
https://github.com/returu/PyTorch常见激活函数:
之前在使用神经网络模型替代线性模型作为逼近函数时,构建神经网络模型时就使用到了一种激活函数Tanh。
【深度学习(PyTorch篇)】22.使用神经网络替换线性模型
Pytorch实现了多种激活函数,一般包含函数形式(torch.relu函数)以及模块形式(torch.nn.ReLU模块)两种形式,可以方便地集成到神经网络模型中。以下是一些常用的激活函数(使用Numpy实现函数功能):
-
Sigmoid函数(torch.nn.Sigmoid):
Sigmoid函数也被称作Logistic函数,是一种常见的S型函数,这也是sigmoid函数的名称的由来(来自希腊字母sigma)。该函数有一个特性,那就是将任何实值映射到范围(0,1)。Sigmoid函数主要用于二分类问题,该函数将一个或多个输入转换为一个概率,其数学表达式为:
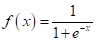
def sigmoid_activation(x):
return 1 / (1 + np.exp(-x))
-
Tanh函数(torch.nn.Tanh):
Tanh函数是双曲线函数的一种,可以说是Sigmoid函数的值域升级版,该函数将任何实值映射到范围(-1,1),其数学表达式为:
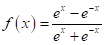
def tanh_activation(x):
return np.tanh(x)
-
ReLU函数(torch.nn.ReLU):
ReLU函数也称作Rectifier函数,该函数非常简单,其实就是求取最大值的函数,如果输入为正数,则原样输出,否则输出为零,其数学表达式为:
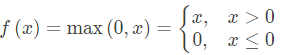
def relu_activation(x):
return np.maximum(0, x)
-
LeakyReLU函数(torch.nn.LeakyReLU):
LeakyReLU函数是ReLU激活函数的一个变体,ReLU输入小于0的部分值都为0,而LeakyReLU输入小于0的部分,值为负,且有微小的梯度。这有助于解决神经元“死亡”问题,即当神经元在训练过程中因为负输入而完全不激活时,会导致权重无法更新。其数学表达式为:
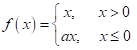
def leaky_relu(x, alpha=0.01):
return np.where(x >= 0, x, alpha * x)
-
Hardtanh函数(torch.nn.Hardtanh):
Hardtanh函数是一种类似于 Tanh 但是计算上更简单的激活函数。与标准的 Tanh 函数相比,Hardtanh 是一种分段线性近似。当输入值在 -1 和 1 之间时,Hardtanh 的输出与输入相同;当输入值小于 -1 时,输出为 -1;当输入值大于 1 时,输出为 1。其数学表达式为:
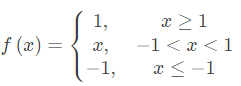
def hardtanh(x):
return np.clip(x, -1, 1)
-
Softplus函数(torch.nn.Softplus):
Softplus函数相当于ReLU 函数的平滑近似,其数学表达式为:
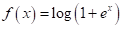
def softplus(x):
return np.log(1 + np.exp(x))
各函数曲线如下图所示:
activation_list = [
sigmoid_activation(input_t),
tanh_activation(input_t),
hardtanh(input_t),
relu_activation(input_t),
leaky_relu(input_t),
softplus(input_t),
]
activation_name_list = [
"Sigmoid",
"Tanh",
"Hardtanh",
"ReLU",
"LeakyReLU",
"Softplus",
]
fig = plt.figure(figsize=(14, 28), dpi=600)
for i, activation_func in enumerate(activation_list):
subplot = fig.add_subplot(len(activation_list), 3, i+1)
subplot.set_title(activation_name_list[i])
output_t = activation_func
plt.grid()
plt.plot(input_t, input_t,'k', linewidth=1)
plt.plot([-3,3], [0,0], 'k', linewidth=1)
plt.plot([0,0], [-3,3], 'k', linewidth=1)
plt.plot(input_t, output_t, 'r', linewidth=3)
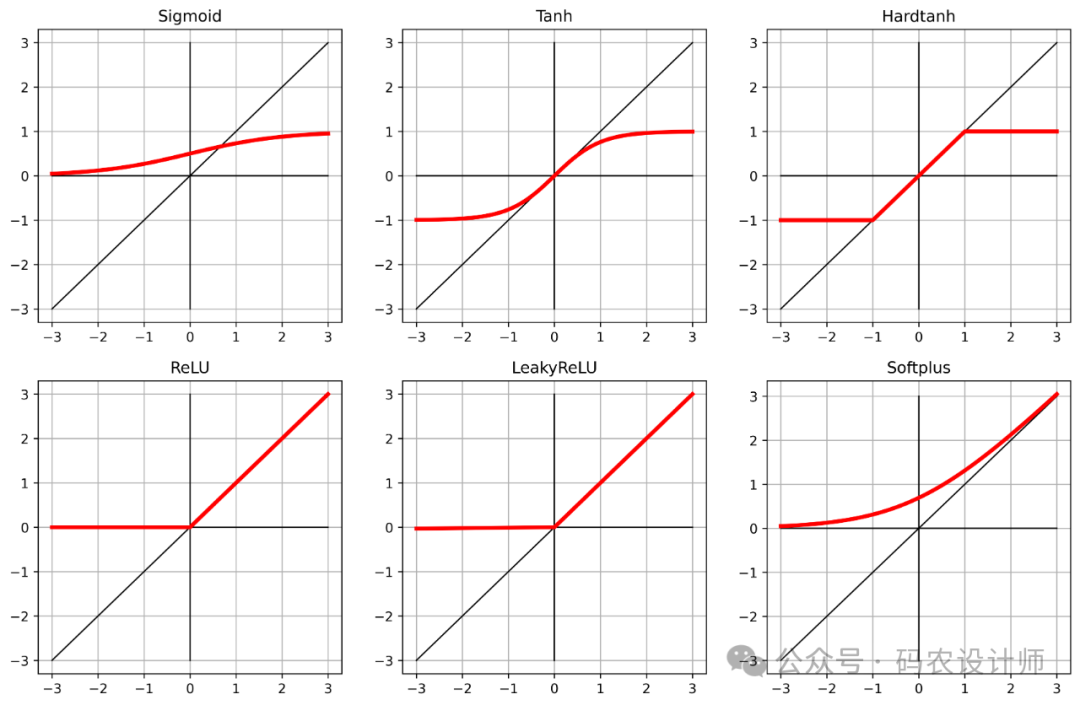
激活函数除去上述几种还有很多,根据具体的应用场景选择合适的激活函数是设计神经网络时的重要步骤,因为它能显著影响模型的性能和学习效果。
-
Softmax函数(torch.nn.Softmax):
Softmax函数也是神经网络中常用的一种激活函数,特别是在处理多分类问题时。它可以将一个向量的元素转换成概率分布,即每个元素的取值范围在 0 到 1 之间,并且所有元素的和为 1。这使得 softmax 函数非常适合用于分类任务中的输出层,因为它可以给出每个类别的预测概率。其数学表达式为:
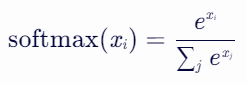
# 示例数据
scores = np.array([[3.0, 1.0, 0.2], [0.5, 2.5, 2.0]])
# python实现
def softmax(x):
"""Compute softmax values for each sets of scores in x."""
result = np.exp(x) / np.exp(x).sum(axis=1, keepdims=True)
return result
softmax(scores)
# 输出结果:
# array([[0.8360188 , 0.11314284, 0.05083836],
# [0.07769558, 0.57409699, 0.34820743]])
# pytorch实现
softmax = torch.nn.Softmax(dim=1)
softmax(torch.tensor(scores))
# 输出结果:
# tensor([[0.8360, 0.1131, 0.0508],
# [0.0777, 0.5741, 0.3482]], dtype=torch.float64)
激活函数的作用:
通过上述列举的一些常用激活函数,可以发现激活函数具有以下特性:
-
激活函数是非线性的,非线性使得神经网络能够拟合任意复杂的函数,极大地提升了模型的表达能力和学习能力。
-
激活函数是可微的,因此在可以通过激活函数计算梯度。
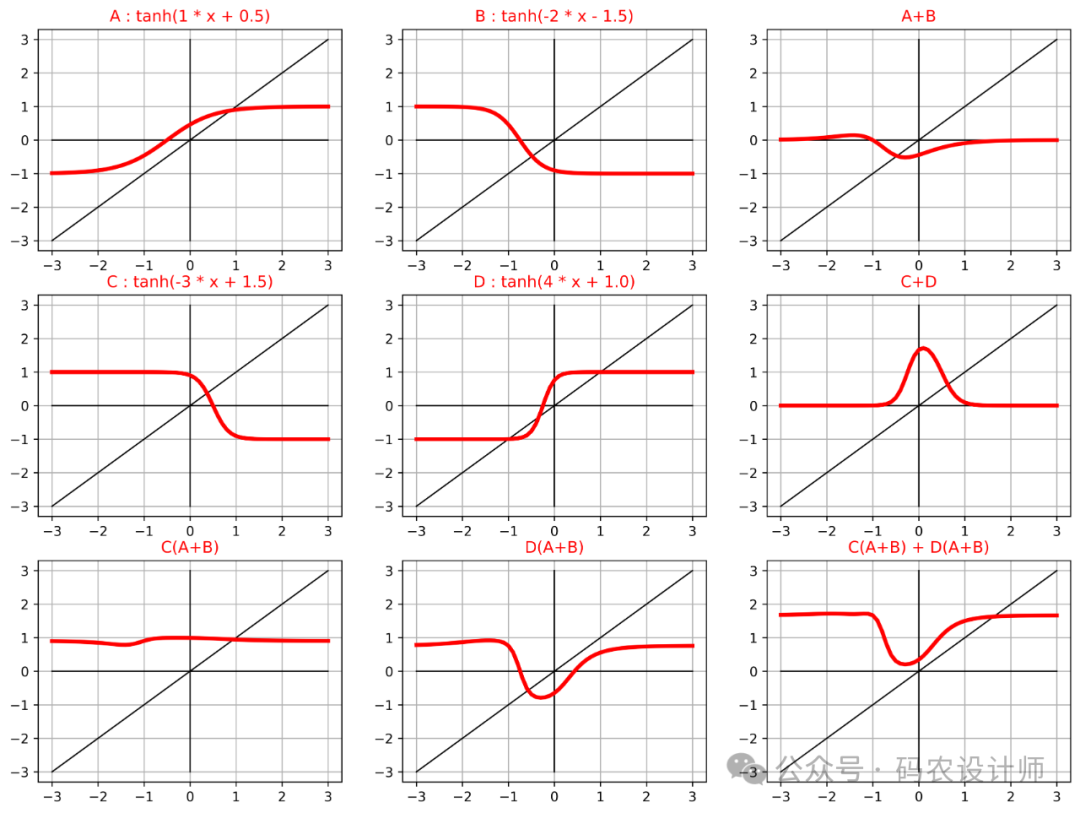
具体代码如下所示:
A = lambda x: tanh_activation(1 * x + 0.5)
B = lambda x: tanh_activation(-2 * x - 1.5)
C = lambda x: tanh_activation(-3 * x + 1.5)
D = lambda x: tanh_activation(4 * x + 1.0)
activation_list = [
(A(input_t),"A : tanh(1 * x + 0.5)"),
(B(input_t),"B : tanh(-2 * x - 1.5)"),
(A(input_t) + B(input_t),"A+B"),
(C(input_t),"C : tanh(-3 * x + 1.5)"),
(D(input_t),"D : tanh(4 * x + 1.0)"),
(C(input_t) + D(input_t),"C+D"),
(C(A(input_t) + B(input_t)),"C(A+B)"),
(D(A(input_t) + B(input_t)),"D(A+B)"),
(C(A(input_t) + B(input_t)) + D(A(input_t) + B(input_t)),"C(A+B) + D(A+B)"),
]
fig = plt.figure(figsize=(14, 32), dpi=600)
for i, (func,name) in enumerate(activation_list):
subplot = fig.add_subplot(len(activation_list), 3, i+1)
subplot.set_title(name,color='red')
output_t = func
plt.grid()
plt.plot(input_t, input_t,'k', linewidth=1)
plt.plot([-3,3], [0,0], 'k', linewidth=1)
plt.plot([0,0], [-3,3], 'k', linewidth=1)
plt.plot(input_t, output_t, 'r', linewidth=3)
Reference: Antiga, Luca Pietro Giovanni, et al. Deep Learning with PyTorch. United States, Manning, 2020.
更多内容可以前往官网查看:
https://pytorch.org/


本篇文章来源于微信公众号: 码农设计师
