本系列文章配套代码获取有以下两种途径:
-
通过百度网盘获取:
链接:https://pan.baidu.com/s/1XuxKa9_G00NznvSK0cr5qw?pwd=mnsj提取码:mnsj
-
前往GitHub获取:
https://github.com/returu/PyTorch卷积层:
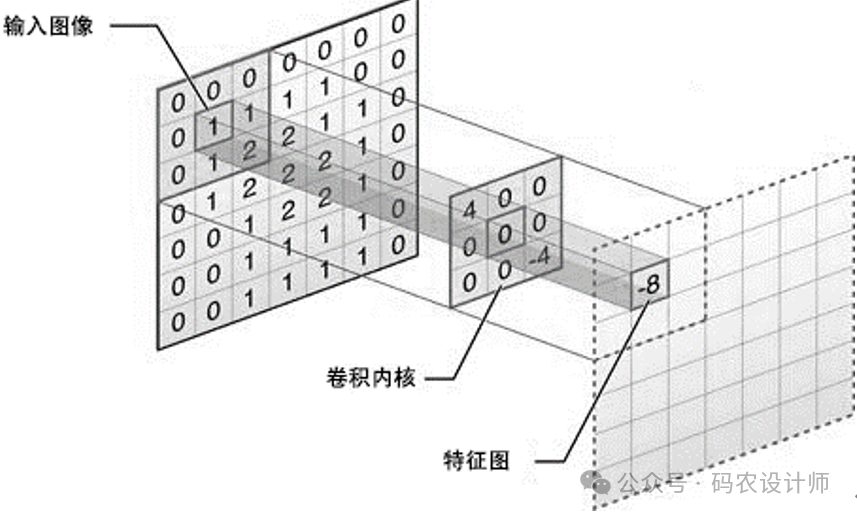
Conv2d:
在Pytorch中,卷积层主要通过torch.nn模块下的Conv1d、Conv2d和Conv3d等类实现,用于处理不同维度的数据。
-
torch.nn.Conv1d:一维卷积层,主要用于时间序列数据,如心电图(ECG)信号。
-
torch.nn.Conv2d:二维卷积层,主要用于图像数据,如RGB图像。
-
torch.nn.Conv3d:三维卷积层,主要用于体数据和视频数据,如医学成像数据(MRI和CT扫描)。
本次以最常使用的torch.nn.Conv2d为例,其构造函数如下:
torch.nn.Conv2d(in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
groups=1,
bias=True,
padding_mode='zeros')
-
in_channels (整数):输入图像的通道数(维度)。例如,RGB图像有3个通道,灰度图像有1个通道。 -
out_channels (整数):输出特征图的通道数,即卷积核的数量。输出图像的通道越多,表示网络的容量越大,借助这些通道能够检测到许多不同类型的特征。 -
kernel_size (整数或元组):卷积核的大小。可以是一个整数(例如,3),表示卷积核的高度和宽度都是该数值;也可以是一个元组(例如,(3, 5)),分别表示卷积核的高度和宽度。 -
stride (整数或元组,可选):卷积步长,默认为1。步长定义了卷积核在图像上移动的速度。与kernel_size类似,它可以是一个整数或一个表示高度和宽度步长的元组。 -
padding (整数或元组,可选):在输入图像周围填充的零的数量,默认为0。填充可以控制输出特征图的大小。它也可以是一个整数或一个表示高度和宽度填充的元组。 -
dilation (整数或元组,可选):卷积核元素之间的间距,默认为1。当dilation大于1时,表示进行空洞卷积(也称为扩张卷积),这可以增加卷积核的感受野而不增加参数数量。 -
groups (整数,可选):控制输入和输出之间的连接。默认为1,表示所有输入通道都连接到每个输出通道。如果groups等于in_channels和out_channels,那么每个输入通道只与对应的输出通道相连,这被称为分组卷积。 -
bias (布尔值,可选):是否添加偏置项到输出中,默认为True。如果设置为False,则不会添加偏置项。 -
padding_mode (字符串,可选):指定填充模式,默认为‘zeros’。其他可选模式包括‘reflect’、‘replicate’和‘circular’。这些模式决定了如何填充输入图像的边界。
在卷积操作中需要知道输出结果的形状,以便设计后续网络结构。卷积操作后的输出形状取决于几个因素:输入的尺寸、卷积核的尺寸、步长(stride)、填充(padding)以及是否使用了dilation。
卷积层的参数为:
-
kernel_size (k_h, k_w):卷积核的高度和宽度。 -
stride (s_h, s_w):卷积核在输入上移动的步长。 -
padding (p_h, p_w):在输入的边界添加的零填充的数量。 -
dilation (d_h, d_w):卷积核元素之间的间距。
输出的高度 H_out 和宽度 W_out 可以按照以下公式计算(⌊ ⌋ 表示向下取整):
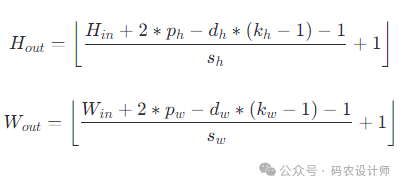
卷积实战:
-
1、随机卷积核:
lena = Image.open('lena.png')
# 将其转换为PyTorch张量
to_tensor = transforms.ToTensor()
lena_tensor = to_tensor(lena).unsqueeze(0)

Lena图原名为“Lenna”,其原型是瑞典模特莱娜·瑟德贝里(Lena Söderberg)。这张图片最初出现在1972年11月的《花花公子》杂志上。由于该图像在视觉上的吸引力和其细节的丰富性,后来被广泛地用作数字图像处理和计算机视觉研究中的标准测试图。
# 创建一个卷积层
# 这里使用5x5的卷积核,输入通道为1,输出通道为3,其他参数使用默认值
conv = nn.Conv2d(1,3,(5,5))
# 权重张量和偏置张量的大小
conv.weight.shape , conv.bias.shape
# 对图像张量进行卷积操作
out = conv(lena_tensor)
# 输出卷积后的结果形状
print("Output shape:", out.shape)
# Output shape: torch.Size([1, 3, 196, 196])
to_pil = transforms.ToPILImage()
out1 = to_pil(out1.squeeze(0))
out2 = to_pil(out2.squeeze(0))
out3 = to_pil(out3.squeeze(0))
# 创建一个一行三列的子图布局
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(15, 5))
# 特征图1
axs[0].imshow(out1,cmap='gray')
axs[0].set_title('channel_1')
axs[0].axis('off') # 关闭坐标轴
# 特征图2
axs[1].imshow(out2,cmap='gray')
axs[1].set_title('channel_2')
axs[1].axis('off')
# 特征图3
axs[2].imshow(out3,cmap='gray')
axs[2].set_title('channel_3')
axs[2].axis('off')

-
2、锐化卷积核:
# 锐化卷积核
kernel = torch.full([3,3],-1.) / 9
kernel[1 ,1] = 1
# 创建一个卷积层
conv = nn.Conv2d(1,1,(3,3),1,bias=False)
# 设置卷积层的权重
conv.weight.data = kernel.reshape(1,1,3,3)
# 对图像张量进行卷积操作
out = conv(lena_tensor)
# 输出卷积后的结果形状
print("Output shape:", out.shape)
# Output shape: torch.Size([1, 1, 198, 198])
# 可视化特征图
to_pil = transforms.ToPILImage()
to_pil(out.squeeze(0))

-
3、填充边界:
padding参数可以接受几种形式的输入:
-
整数:表示在所有四个边缘(顶部、底部、左侧、右侧)都添加相同数量的零填充。 -
元组:如果提供两个整数的元组,第一个整数表示垂直方向(高度)的填充,第二个整数表示水平方向(宽度)的填充。如果提供四个整数的元组,则它们分别对应于(左、右、顶、底)的填充。
假设我们有一个3×3的输入矩阵,然后使用padding=1,那么首先会在输入矩阵的四周各添加一个像素宽的零填充,得到一个新的5×5矩阵,然后在进行卷积操作。
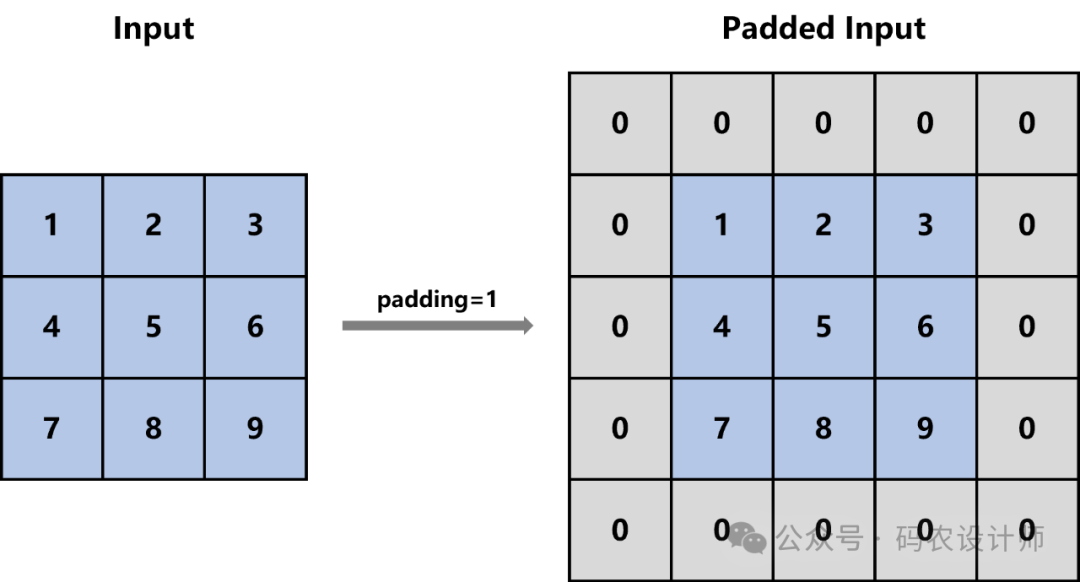
# 创建一个卷积层
# 这里使用5x5的卷积核,输入通道为1,输出通道为3,填充为2,其他参数使用默认值
conv = nn.Conv2d(1,3,(5,5),padding=2)
# 对图像张量进行卷积操作
out = conv(lena_tensor)
# 输出卷积后的结果形状
print("Output shape:", out.shape)
# Output shape: torch.Size([1, 3, 200, 200])
更多内容可以前往官网查看:
https://pytorch.org/


本篇文章来源于微信公众号: 码农设计师
