本系列配套练习数据下载链接:
链接:https://pan.baidu.com/s/1imKDcw9wZWk_ItR8fwugZw?pwd=mnsj提取码:mnsj
聚类分布制图工具集可通过执行聚类分析来识别具有统计显著性的热点、冷点和空间异常值的位置。这些工具在需要根据一个或多个聚类的位置执行某些行动时特别有用,例如在需要分配更多的警力来处理一组集中出现的入室盗窃案时,或者需要确定疾病爆发的地点以找到疾病根源的线索时。
聚类分布制图工具集包含聚类和异常值分析、分组分析、热点分析、优化的热点分析、优化的异常值分析、相似搜索六个工具。
本次主要介绍热点分析(Getis-Ord Gi*)工具。
-
1、概念:
热点分析(Getis-Ord Gi*)工具用于识别数据中具有统计显著性的热点和冷点。
该工具会对数据集中的每一个要素计算Getis-Ord Gi*统计量,这是一种局部统计量,用于量化一个地区要素值与邻近地区相比是否显著地高或低。具体来说,该工具会查看邻近要素环境中的每一个要素。一个要素要成为具有显著统计意义的热点,不仅需要具有高值,而且还需要被其他同样具有高值的要素所包围。如果应用FDR校正,统计显著性还会根据多重测试和空间依赖性进行调整。
该工具的输出结果通常是一个新的要素类,其中每个要素都具有z得分、p值和置信区间(Gi_Bin字段)等属性。这些属性可以帮助用户直观地了解哪些区域是热点,哪些是冷点,并且可以根据需要将这些结果进行可视化展示。
-
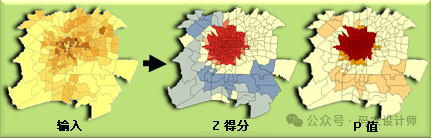
z 得分:z得分是标准差的倍数,表示观察到的空间聚类与随机分布之间的差异程度。正的z得分表示高值的空间聚类(热点),而负的z得分则表示低值的空间聚类(冷点)。z得分的绝对值越大,表示观测到的聚类越显著,即热点或冷点越强烈。
-
p 值:用于检验观测到的空间聚类是否显著,即检验零假设(没有空间聚类)是否可以被拒绝。一个较小的p值(通常小于0.05或0.01)表示我们可以有很高的信心拒绝零假设,认为观测到的空间聚类是显著的,而非随机产生的。p值越小,观测到的聚类越不可能是由随机过程产生的,因此越显著。需要注意的是,在没有 FDR 校正的情况下,统计显著性以 p 值和 z 得分字段为基础。如果选中可选参数应用错误发现率(FDR)校正,确定置信度的关键 p 值会降低以兼顾多重测试和空间依赖性。
-
置信区间(Gi_Bin字段):用于表示统计显著性的水平。通常,置信区间会根据z得分被划分为几个不同的类别,置信区间 +3 到 -3 中的要素反映置信度为 99% 的统计显著性;置信区间 +2 到 -2 中的要素反映置信度为 95% 的统计显著性;置信区间 +1 到 -1 中的要素反映置信度为 90% 的统计显著性;而置信区间 0 中要素的聚类则没有统计学意义。
—————-
-
2、工具:
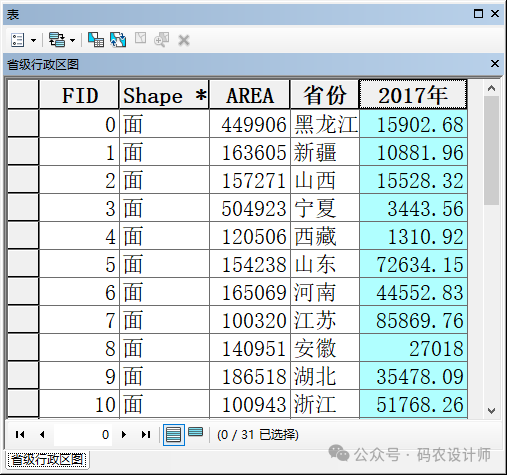
-
输入字段:用于计算的数值字段。输入字段应包含多种值。此统计数学方法要求待分析的变量存在一定程度的变化;例如,如果所有输入都是 1 便无法求解; -
空间关系的概念化:指定要素空间关系的定义方式,即空间权重关系; -
距离法:指定计算每个要素与邻近要素之间的距离的方式。选项包括欧氏距离以及曼哈顿距离; -
距离范围或距离阈值:为“反距离”和“固定距离”选项指定中断距离。将在对目标要素的分析中忽略为该要素指定的中断之外的要素。但是,对于“无差别的区域”,指定距离之外的要素的影响会随距离的减小而变弱,而在距离阈值之内的影响则被视为是等同的; -
自然电位字段:此字段表示自身潜力,要素与其自身之间的距离或权重。 -
应用错误发现率(FDR)校正:指定在评估统计显著性时是否使用 FDR 校正。选中时,统计显著性将以错误发现率校正为基础。未选中时(默认设置),统计显著性将以 p 值和 z 得分字段为基础。
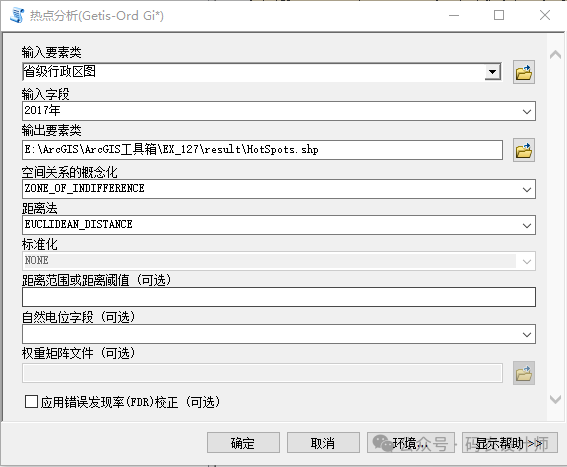
点击确定,通过输出的结果图层可以看出,2017年全国经济热点区域主要集中在东部沿海地区,青海和西藏为冷点区域。
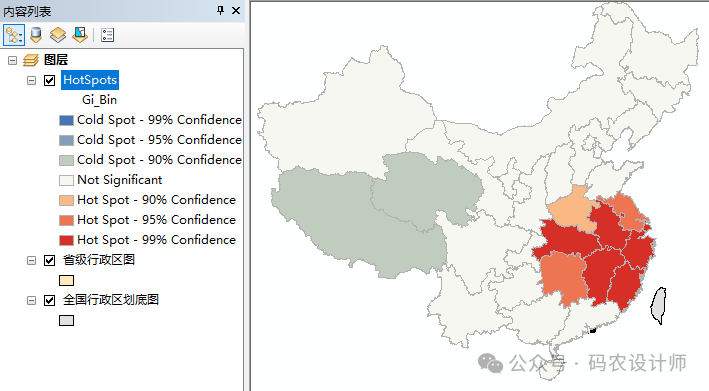
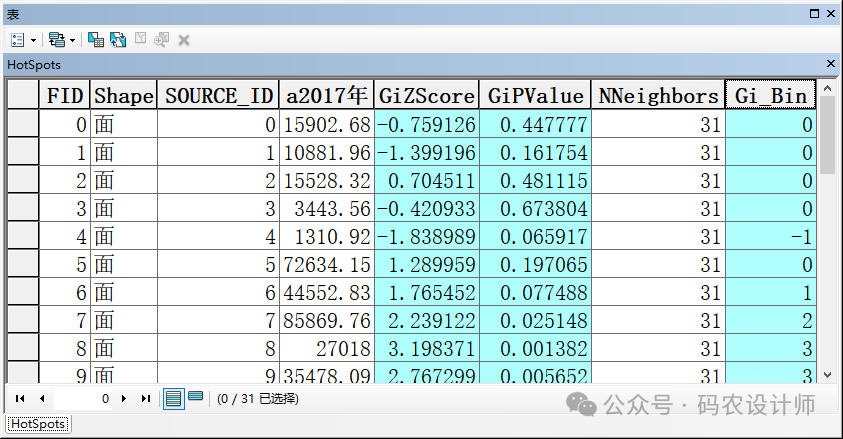
打开结果图层的属性表,可以看到计算得到的Z得分、P值和Gi_Bin(置信区间)等字段。其中,Gi_Bin字段值代表具有统计显著性的热点和冷点区域,Gi_Bin字段值在[-3,3]中的要素置信度为99%的统计显著性、在[-2,2]中的要素置信度为95%的统计显著性、在[-1,1]中的要素置信度为90%的统计显著性,Gi_Bin字段值为0代表没有显著的统计学意义。


本篇文章来源于微信公众号: 码农设计师
