本系列文章配套代码获取有以下三种途径:
-
可以在以下网站查看,该网站是使用JupyterLite搭建的web端Jupyter环境,因此无需在本地安装运行环境即可使用,首次运行浏览器需要下载一些配置文件(大约20M):
https://returu.github.io/Python_Data_Analysis/lab/index.html-
也可以通过百度网盘获取,需要在本地配置代码运行环境,环境配置可以查看【Python基础】2.搭建Python开发环境:
链接:https://pan.baidu.com/s/1MYkeYeVAIRqbxezQECHwcA?pwd=mnsj提取码:mnsj
-
前往GitHub详情页面,单击 code 按钮,选择Download ZIP选项:
https://github.com/returu/Python_Data_Analysis根据《Python for Data Analysis 3rd Edition》翻译整理
—————————————————–
statsmodels(https://www.statsmodels.org/stable/index.html) 是一个Python库,用于拟合多种统计模型,进行统计测试、数据探索和可视化,可以使用conda安装:conda install statsmodels。
statsmodels中包括以下一些模型:
-
线性模型、广义线性模型和鲁棒线性模型;
-
线性混合效应模型;
-
方差分析(ANOVA)方法;
-
时间序列过程和状态空间模型;
-
广义矩量法。
statsmodels中的线性回归模型有多种,从基本的(如普通最小二乘法)到复杂的(如迭代重新加权的最小二乘法)。
statsmodels中的线性模型有两个不同的主要接口:基于数组和基于公式。这些接口都是通过以下API模块导入访问的。
1import statsmodels.api as sm
2import statsmodels.formula.api as smf
首先我们根据一些随机数据生成一个线性模型:
1# 定义随机种子,使得结果可重复
2rng = np.random.default_rng(seed=12345)
3
4# 定义一个用于生成具有特定均值和方差的正态分布数据的辅助函数
5def dnorm(mean, variance, size=1):
6 if isinstance(size, int):
7 size = size,
8 return mean + np.sqrt(variance) * rng.standard_normal(*size)
9
10N = 100
11# np.c_ 用于连接多个矩阵,X的shape为(100,3)
12X = np.c_[dnorm(0, 0.4, size=N),
13 dnorm(0, 0.6, size=N),
14 dnorm(0, 0.2, size=N)]
15eps = dnorm(0, 0.1, size=N)
16beta = [0.1, 0.3, 0.5]
17
18y = np.dot(X, beta) + eps # 已知参数beta的 "真实 "模型
线性模型一般是用截距项来拟合的,sm.add_constant 函数可以在现有的矩阵中添加截距项。
1X_model = sm.add_constant(X)
m.OLS类可以拟合一个普通最小二乘法的线性回归。
1model = sm.OLS(y, X)
模型的 fit 方法返回一个包含估计的模型参数和其他诊断的回归结果对象。
1results = model.fit()
2results.params # array([0.06681503, 0.26803235, 0.45052319])
在 results 上调用 summary 方法可以打印一个模型的详细诊断输出。
1print(results.summary())
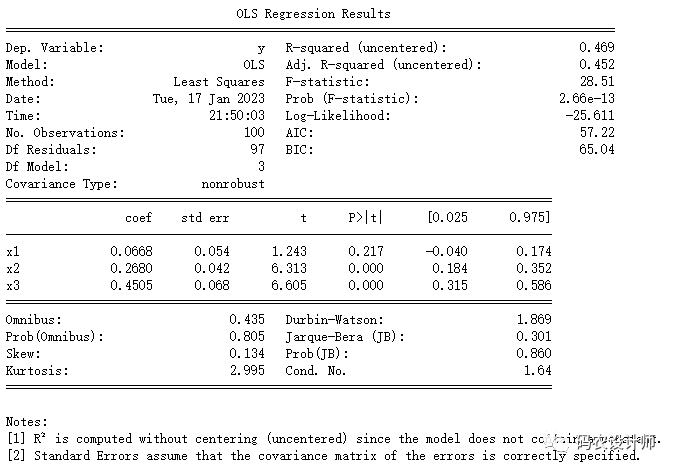
上述输出中的参数名称已经被赋予了通用名称 x1,x2,等等。假设所有的模型参数都在一个DataFrame中。
1data = pd.DataFrame(X, columns=['col0', 'col1', 'col2'])
2
3data['y'] = y
4
5data[:5]
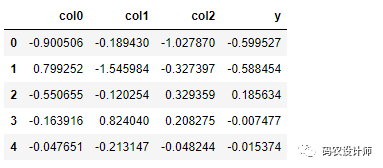
现在我们可以使用statsmodels公式API和Patsy公式字符串。在使用公式和pandas对象时,我们也不需要使用add_constant。
1results = smf.ols('y ~ col0 + col1 + col2', data=data).fit()
2
3results.params
4# Intercept -0.020799
5# col0 0.065813
6# col1 0.268970
7# col2 0.449419
8# dtype: float64
9
10results.tvalues
11# Intercept -0.652501
12# col0 1.219768
13# col1 6.312369
14# col2 6.567428
15# dtype: float64
给定新的样本外数据后,可以计算出给定的模型参数的预测值。
1results.predict(data[:5])
2# 0 -0.592959
3# 1 -0.531160
4# 2 0.058636
5# 3 0.283658
6# 4 -0.102947
7# dtype: float64
在statsmodels中,还有许多额外的工具用于线性模型结果的分析、诊断和可视化。除了普通最小二乘法,还有其他类型的线性模型。
statsmodels中的另一类模型是用于时间序列分析的。其中有自回归过程、卡尔曼滤波和其他状态空间模型,以及多变量自回归模型。
首先模拟生成一些具有自回归结构和噪声的时间序列数据:
1init_x = 4
2
3values = [init_x, init_x]
4N = 1000
5
6b0 = 0.8
7b1 = -0.4
8noise = dnorm(0, 0.1, N)
9for i in range(N):
10 new_x = values[-1] * b0 + values[-2] * b1 + noise[i]
11 values.append(new_x)
这个数据有一个AR(2)结构(两个滞后期),参数为0.8和-0.4。当你拟合一个AR模型时,你可能不知道要包括多少个滞后项,所以你可以用一些更大的滞后项来拟合模型。
1from statsmodels.tsa.ar_model import AutoReg
2
3MAXLAGS = 5
4
5model = AutoReg(values, MAXLAGS)
6
7results = model.fit()
8
9# 结果中的估计参数首先是截距,然后是前两个滞后期的估计值。
10results.params
11# array([ 0.02346612, 0.8096828 , -0.42865278, -0.03336517, 0.04267874, -0.05671529])
这些模型的更深层次的细节以及如何解释它们的结果,可以在statsmodels文档中查看。
本篇文章来源于微信公众号: 码农设计师
