本系列文章是根据Shapely官方文档翻译整理,学习任何一个Python第三方库,其官方文档都是最好的学习资料。相比网络搜索得到的一些资料,官方文档是权威的一手资料,其内容全面、准确可靠。通过官方文档入手,能够保证学习认知不会有大偏差。在学习完官方文档后,可以在寻找其他资料进一步学习。
点击“阅读原文”或者直接访问下方链接,查看翻译整理的“Shapely 2.0.0 中文文档”。
https://www.mizhushare.com/docs/shapely-2-0-0-%e4%b8%ad%e6%96%87%e6%96%87%e6%a1%a3/-
可以通过百度网盘获取,需要在本地配置代码运行环境:
链接:https://pan.baidu.com/s/1iWGGhB4kra9V7bUj-CWR0w?pwd=mnsj提取码:mnsj
-
前往GitHub详情页面,单击 code 按钮,选择Download ZIP选项:
https://github.com/returu/Shapely-
shapely.ops.clip_by_rect():
1shapely.ops.clip_by_rect(geom, xmin, ymin, xmax, ymax)
返回一个几何对象在矩形内的部分。几何对象会以一种快速但可能是粗糙的方式被剪掉。
需要注意的是,输出不保证是有效的。对于拓扑结构的错误,将不会产生异常。
1>>> from shapely.ops import clip_by_rect
2
3>>> polygon = Polygon(shell=[(0, 0), (0, 30), (30, 30), (30, 0), (0, 0)],
4... holes=[[(10, 10), (20, 10), (20, 20), (10, 20), (10, 10)]])
5>>> polygon
6<POLYGON ((0 0, 0 30, 30 30, 30 0, 0 0), (10 10, 20 10, 20 20, 10 20, 10 10))>
7
8# 矩形剪裁
9>>> clipped_polygon = clip_by_rect(polygon , 5,5,15,15)
10>>> clipped_polygon
11<POLYGON ((5 5, 5 15, 10 15, 10 10, 15 10, 15 5, 5 5))>
裁剪结果如下图所示(灰色为原始几何对象,红色部分为裁剪结果):
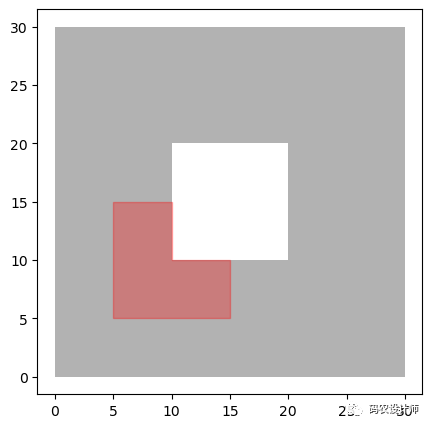
2.高效合并:
-
shapely.ops.unary_union(geoms):
返回给定几何对象的合并结果。
shapely.ops中的unary_union()函数比union()的效率更高。
重叠的多边形区域将被合并。线将被完全溶解和节点化。重复的点将被合并。
1>>> from shapely.ops import unary_union
2
3>>> polygons = [Point(i,0).buffer(0.7) for i in range(5)]
4>>> polygons
5[<POLYGON ((0.7 0, 0.697 -0.069, 0.687 -0.137, 0.67 -0.203, 0.647 -0.268, 0.6...>, <POLYGON ((1.7 0, 1.697 -0.069, 1.687 -0.137, 1.67 -0.203, 1.647 -0.268, 1.6...>, <POLYGON ((2.7 0, 2.697 -0.069, 2.687 -0.137, 2.67 -0.203, 2.647 -0.268, 2.6...>, <POLYGON ((3.7 0, 3.697 -0.069, 3.687 -0.137, 3.67 -0.203, 3.647 -0.268, 3.6...>, <POLYGON ((4.7 0, 4.697 -0.069, 4.687 -0.137, 4.67 -0.203, 4.647 -0.268, 4.6...>]
6
7# 合并操作
8>>> unary_union(polygons)
9<POLYGON ((0.444 -0.541, 0.389 -0.582, 0.33 -0.617, 0.268 -0.647, 0.203 -0.6...>
裁剪结果如下图所示(左图为原始几何对象,右图为合并结果):

从上述示例中,可以看到unary_union()函数合并了重叠的多边形区域,所以该方法可以用来修复无效的多边形。与零距离buffer()操作的技巧一样,在使用这个方法时,依实际情况可能有差别。
1>>> m = MultiPolygon(polygons)
2>>> m
3<MULTIPOLYGON (((0.7 0, 0.697 -0.069, 0.687 -0.137, 0.67 -0.203, 0.647 -0.26...>
4>>> m.area
57.684543801837549
6>>> m.is_valid
7False
8
9# unary_union()操作
10>>> unary_union(m).area
116.610301355116799
12>>> unary_union(m).is_valid
13True
3.狄洛尼三角剖分:
-
shapely.ops.triangulate(geom, tolerance=0.0, edges=False):
返回输入几何对象的狄洛尼三角剖分图。
输入可以是任何几何对象类型,该几何对象的所有顶点都将被用作三角形的点。
tolerance参数的设置用于提高三角计算的稳健性,容差为0.0表示不进行捕获。
如果edges参数为False,将返回三角形Polygon的列表,否则将返回一个边界LineString的列表。
1>>> from shapely.ops import triangulate
2
3>>> points = MultiPoint([(0, 0), (1, 1), (0, 2), (2, 2), (3, 1), (1, 0)])
4>>> points
5<MULTIPOINT (0 0, 1 1, 0 2, 2 2, 3 1, 1 0)>
6
7# edges参数默认为False,结果将返回三角形polygon的列表
8>>> triangulate(points)
9[<POLYGON ((0 2, 0 0, 1 1, 0 2))>, <POLYGON ((0 2, 1 1, 2 2, 0 2))>, <POLYGON ((2 2, 1 1, 3 1, 2 2))>, <POLYGON ((3 1, 1 1, 1 0, 3 1))>, <POLYGON ((1 0, 1 1, 0 0, 1 0))>]
结果如下图所示:
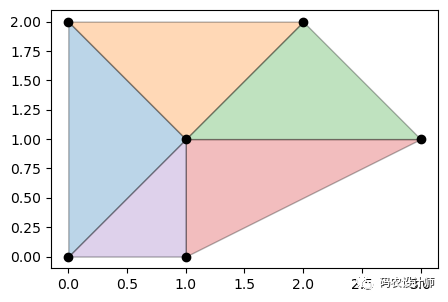
edges参数默认为True时,结果将返回三角形边界的列表:
1>>> triangulate(points , edges=True)
2[<LINESTRING (2 2, 3 1)>, <LINESTRING (0 2, 2 2)>, <LINESTRING (0 0, 0 2)>, <LINESTRING (0 0, 1 0)>, <LINESTRING (1 0, 3 1)>, <LINESTRING (1 0, 1 1)>, <LINESTRING (1 1, 3 1)>, <LINESTRING (1 1, 2 2)>, <LINESTRING (0 2, 1 1)>, <LINESTRING (0 0, 1 1)>]
结果如下图所示:
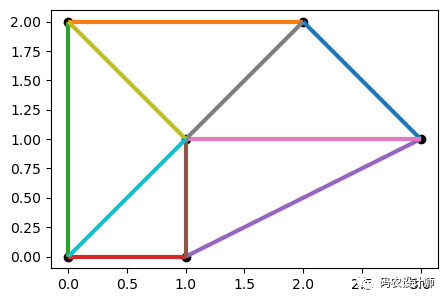
4.泰森多边形:
-
shapely.ops.voronoi_diagram(geom, envelope=None, tolerance=0.0, edges=False):
通过输入几何对象的顶点构建一个泰森多边形。
输入可以是任何几何对象类型。该几何对象的所有顶点都将被用作图表的输入点。
envelope关键字参数提供了一个用于裁剪结果图的外包矩形。如果没有,它将被自动计算。图表将被裁剪到所提供的包络矩形或围绕这些点的包络矩形中较大的一个。
tolerance参数的设置用于提高计算稳健性,容差参数为0.0表示不进行捕获。容差参数可能很不稳定,已知在一些情况下会导致算法失败。如果你正在使用容差参数并计算失败,试着去掉它。
如果edges参数为False,将返回Polygon列表。否则将返回一个LineString边界的列表。
1>>> from shapely.ops import voronoi_diagram
2
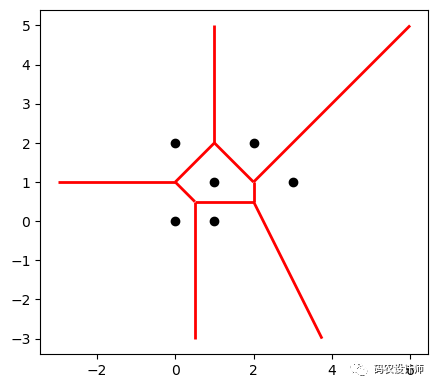
3>>> points = MultiPoint([(0, 0), (1, 1), (0, 2), (2, 2), (3, 1), (1, 0)])
4>>> points
5<MULTIPOINT (0 0, 1 1, 0 2, 2 2, 3 1, 1 0)>
6
7# edges参数默认为False,结果将返回三角形polygon的列表
8>>> regions = voronoi_diagram(points)
9>>> regions
10<GEOMETRYCOLLECTION (POLYGON ((2 1, 2 0.5, 0.5 0.5, 0 1, 1 2, 2 1)), POLYGON...>
11>>> list(regions.geoms)
12[<POLYGON ((2 1, 2 0.5, 0.5 0.5, 0 1, 1 2, 2 1))>, <POLYGON ((6 -3, 3.75 -3, 2 0.5, 2 1, 6 5, 6 -3))>, <POLYGON ((-3 -3, -3 1, 0 1, 0.5 0.5, 0.5 -3, -3 -3))>, <POLYGON ((0.5 -3, 0.5 0.5, 2 0.5, 3.75 -3, 0.5 -3))>, <POLYGON ((-3 5, 1 5, 1 2, 0 1, -3 1, -3 5))>, <POLYGON ((6 5, 2 1, 1 2, 1 5, 6 5))>]
13>>> len(regions.geoms)
146结果如下图所示:
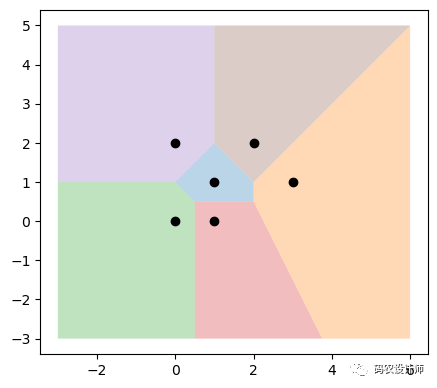
edges参数默认为True时,结果将返回多边形边界的列表:
1>>> regions_2 = voronoi_diagram(points , edges=True)
2>>> regions_2
3<GEOMETRYCOLLECTION (MULTILINESTRING ((2 1, 2 0.5), (2 0.5, 0.5 0.5), (0.5 0...>
4>>> list(regions_2.geoms)
5[<MULTILINESTRING ((2 1, 2 0.5), (2 0.5, 0.5 0.5), (0.5 0.5, 0 1), (0 1, 1 2)...>]
6>>> len(regions_2.geoms)
71
结果如下图所示:

END

本篇文章来源于微信公众号: 码农设计师
