本系列文章是根据Shapely官方文档翻译整理,学习任何一个Python第三方库,其官方文档都是最好的学习资料。相比网络搜索得到的一些资料,官方文档是权威的一手资料,其内容全面、准确可靠。通过官方文档入手,能够保证学习认知不会有大偏差。在学习完官方文档后,可以在寻找其他资料进一步学习。
点击“阅读原文”或者直接访问下方链接,查看翻译整理的“Shapely 2.0.0 中文文档”。
https://www.mizhushare.com/docs/shapely-2-0-0-%e4%b8%ad%e6%96%87%e6%96%87%e6%a1%a3/-
可以通过百度网盘获取,需要在本地配置代码运行环境:
链接:https://pan.baidu.com/s/1iWGGhB4kra9V7bUj-CWR0w?pwd=mnsj提取码:mnsj
-
前往GitHub详情页面,单击 code 按钮,选择Download ZIP选项:
https://github.com/returu/Shapely1.最近的点:
-
shapely.ops.nearest_points(geom1, geom2):
返回输入几何对象中最近的一组点组成的元组。这些点的返回顺序与输入几何对象的顺序相同。
1>>> from shapely.ops import nearest_points
2
3>>> triangle = Polygon([(0, 0), (1, 0), (0.5, 1), (0, 0)])
4>>> triangle
5<POLYGON ((0 0, 1 0, 0.5 1, 0 0))>
6>>> square = Polygon([(0, 2), (1, 2), (1, 3), (0, 3), (0, 2)])
7>>> square
8<POLYGON ((0 2, 1 2, 1 3, 0 3, 0 2))>
9
10# 计算两个几何对象最近的一组点
11>>> result = nearest_points(triangle , square)
12>>> result
13(<POINT (0.5 1)>, <POINT (0.5 2)>)
结果如下图所示:

2.对齐:
-
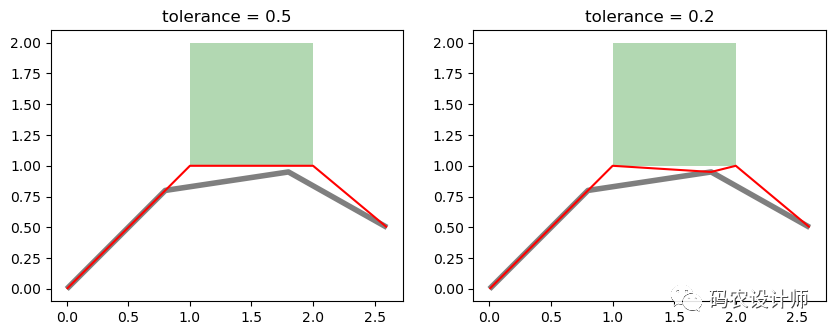
shapely.ops.snap(geom1, geom2, tolerance):
将geom1中的顶点与geom2中的顶点对齐,被捕捉的几何体对象副本会被返回,输入的几何对象不会被修改。
tolerance参数指定了执行对齐操作的顶点之间的最小距离。
1>>> from shapely.ops import snap
2
3>>> square = Polygon([(1,1), (2, 1), (2, 2), (1, 2), (1, 1)])
4>>> square
5<POLYGON ((1 1, 2 1, 2 2, 1 2, 1 1))>
6>>> line = LineString([(0,0), (0.8, 0.8), (1.8, 0.95), (2.6, 0.5)])
7>>> line
8<LINESTRING (0 0, 0.8 0.8, 1.8 0.95, 2.6 0.5)>
9
10# tolerance = 0.5
11>>> result1 = snap(line , square , 0.5)
12>>> result1
13<LINESTRING (0 0, 1 1, 2 1, 2.6 0.5)>
14
15# tolerance = 0.2
16>>> result2 = snap(line , square , 0.2)
17>>> result2
18<LINESTRING (0 0, 0.8 0.8, 1 1, 1.8 0.95, 2 1, 2.6 0.5)>
结果如下图所示:
3.共享路径:
-
shapely.ops.shared_paths(geom1, geom2):
找geom1和geom2之间的共享路径,返回一个有两个元素的几何集合,其中两个几何对象都是LineString类型。
-
第一个元素是一个MultiLineString,包含两个输入方向相同的共享路径。 -
第二个元素是一个MultiLineString,包含两个输入方向相反的共享路径。
1>>> from shapely.ops import shared_paths
2
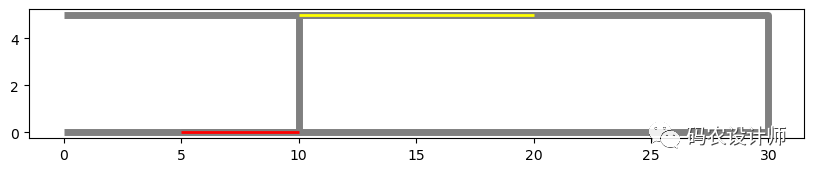
3>>> g1 = LineString([(0, 0), (10, 0), (10, 5), (20, 5)])
4>>> g1
5<LINESTRING (0 0, 10 0, 10 5, 20 5)>
6>>> g2 = LineString([(5, 0), (30, 0), (30, 5), (0, 5)])
7>>> g2
8<LINESTRING (5 0, 30 0, 30 5, 0 5)>

以上述几何对象为例,求解共享路径:
1>>> shared_paths(g1 , g2)
2<GEOMETRYCOLLECTION (MULTILINESTRING ((5 0, 10 0)), MULTILINESTRING ((10 5, ...>
3
4>>> forward , backward = shared_paths(g1 , g2).geoms
5>>> forward
6<MULTILINESTRING ((5 0, 10 0))>
7>>> backward
8<MULTILINESTRING ((10 5, 20 5))>
结果如下图所示,其中,灰色线为原几何对象,红色线为与两个输入方向相同的共享路径。黄色线为与两个输入方向相反的共享路径:
4.分割:
-
shapely.ops.split(geom, splitter):
将一个几何对象与另一个几何对象分割,并返回一个几何集合。
该函数在理论上与分割后的几何对象部分的联合操作相反。如果分割器没有分割几何对象,则返回一个与输入几何对象相同的单一几何集合。
以较低的容差分割几何对象可能是很方便的。例如,在用一个点分割线的情况下,该点必须正好在直线上,才能正确分割直线。当用多边形分割一条线时,多边形的边界被用于运算。当用另一条线分割一条线时,如果这两条线在某些段上重叠,就会产生ValueError。
首先生成一个点和一条线两个几何对象:
1>>> from shapely.ops import split
2
3>>> point = Point((1, 1))
4>>> line = LineString([(0,0), (2,2)])
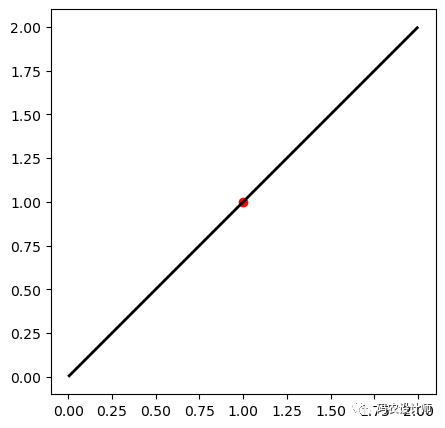
然后,用点来分割线:
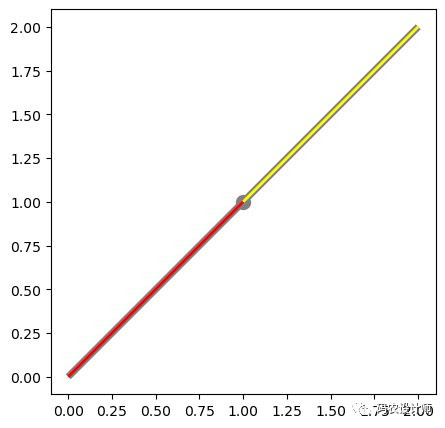
1>>> result = split(line , point)
2>>> result
3<GEOMETRYCOLLECTION (LINESTRING (0 0, 1 1), LINESTRING (1 1, 2 2))>
4>>> list(result.geoms)
5[<LINESTRING (0 0, 1 1)>, <LINESTRING (1 1, 2 2)>]
结果如下图所示,其中,灰色线和灰色点为原几何对象,黄色线和红色线为分割结果:

END

本篇文章来源于微信公众号: 码农设计师
