本系列文章是根据Shapely官方文档翻译整理,学习任何一个Python第三方库,其官方文档都是最好的学习资料。相比网络搜索得到的一些资料,官方文档是权威的一手资料,其内容全面、准确可靠。通过官方文档入手,能够保证学习认知不会有大偏差。在学习完官方文档后,可以在寻找其他资料进一步学习。
点击“阅读原文”或者直接访问下方链接,查看翻译整理的“Shapely 2.0.0 中文文档”。
https://www.mizhushare.com/docs/shapely-2-0-0-%e4%b8%ad%e6%96%87%e6%96%87%e6%a1%a3/-
可以通过百度网盘获取,需要在本地配置代码运行环境:
链接:https://pan.baidu.com/s/1iWGGhB4kra9V7bUj-CWR0w?pwd=mnsj提取码:mnsj
-
前往GitHub详情页面,单击 code 按钮,选择Download ZIP选项:
https://github.com/returu/ShapelyShapely中几何对象是以典型的 Python 方式创建的,即使用类来实例化。
例如,
点状集合要素通过 class Point(coordinates) 实例化;
线状几何要素通过 class LineString(coordinates) 实例化;
线环几何要素通过 classLinearRing(coordinates) 实例化;
多边形几何要素通过 class Polygon(shell [, holes=None]) 实例化。
Point、LineString等实例最重要的属性是一个决定了其的内部、边界和外部点集的有限序列的坐标 coordinates,坐标序列是不可改变的。
1# 点的实例化
2>>> from shapely import Point
3>>> point = Point(0, 0)
4>>> point
5<POINT (0 0)>
6
7# 线的实例化
8>>> from shapely import LineString
9>>> line = LineString([(0, 0), (1, 1)])
10>>> line
11<LINESTRING (0 0, 1 1)>
12
13# 面的实例化
14>>> from shapely import Polygon
15>>> polygon = Polygon([(0, 0), (1, 1), (1, 0)])
16>>> polygon
17<POLYGON ((0 0, 1 1, 1 0, 0 0))>
Shapely是一个平面几何库,在几何分析中忽略了z,即平面上或平面下的高度。在构造实例时可以使用第三维 Z 坐标值,但对几何分析没有影响。所有操作都在x-y二维平面内进行。
1# 三维点的实例化
2>>> point = Point(0, 0 , 1)
3>>> point
4<POINT Z (0 0 1)>
需要注意的是,这里会有一个潜在的问题:只在 z 上有差异的坐标图元是不能相互区分的,它们的应用会导致无效的几何对象。例如,LineString([(0, 0, 0), (0, 0, 1)]) 不会返回一条单位长度的垂直线,而是返回平面内一条长度为零的无效线。同样,Polygon([(0, 0, 0), (0, 0, 1), (1, 1, 1)]) 没有被一个封闭的环所包围,是无效的。
在所有的构造函数中,数字值会被转换为float浮点类型。换句话说,Point(0, 0)和Point(0.0, 0.0)会产生等同的几何实例。Shapely在构造实例时不检查其拓扑结构的有效性,因为在大多数情况下是不必要的。可以使用 :attr:is_valid 谓词对几何实例的有效性进行验证。
1>>> Point(0, 0) == Point(0.0, 0.0)
2True首先分别实例化一个点、线、面几何对象:
1>>> point = Point(0, 0)
2>>> line = LineString([(0, 0), (1, 1)])
3>>> polygon = Polygon([(0, 0), (1, 1), (1, 0)])
下面是Shapely几何对象的通用属性和方法(object为一几何对象):
-
object.area—— 返回几何对象的面积(浮点类型)。
1>>> point.area , line.area , polygon.area
2(0.0, 0.0, 0.5)
-
object.length—— 返回几何对象的长度(浮点类型)。
1>>> point.length , line.length , polygon.length
2(0.0, 1.4142135623730951, 3.414213562373095)
-
object.bounds—— 返回一个表示几何对象边界的元祖(minx, miny, maxx, maxy),即最小外包矩形。
1>>> point.bounds , line.bounds , polygon.bounds
2((0.0, 0.0, 0.0, 0.0), (0.0, 0.0, 1.0, 1.0), (0.0, 0.0, 1.0, 1.0))
-
object.minimum_clearance—— 返回一个节点被移动以产生一个无效的几何形状的最小距离。这可以被认为是衡量一个几何体稳健性的标准,较大的最小间隙值表明一个更稳健的几何体。如果一个几何体不存在最小间隙,例如一个点,这将返回math.infinity。
1>>> polygon = Polygon([(0, 0), (2, 0), (2, 1), (0, 1), (0, 0)])
2>>> polygon
3<POLYGON ((0 0, 2 0, 2 1, 0 1, 0 0))>
4>>> polygon.minimum_clearance # 结果为长方形的短边长度
51.0
6
7>>> polygon2 = Polygon([(0, 0), (1, 1), (1, 0)])
8>>> polygon2
9<POLYGON ((0 0, 1 1, 1 0, 0 0))>
10>>> polygon2.minimum_clearance # 结果为三角形中长边垂线段的长度值
110.7071067811865476
12
13# 点将返回math.infinity
14>>> point = Point(0, 0)
15>>> point.minimum_clearance
16inf
17
18# 线的结果为线段长度
19>>> line = LineString([(0, 0), (1, 1)])
20>>> line.minimum_clearance
211.4142135623730951
-
object.geom_type—— 返回一个字符串,根据OpenGIS的格式标准指定对象的几何类型。
1>>> point.geom_type
2'Point'
3
4>>> line.geom_type
5'LineString'
6
7>>> polygon.geom_type
8'Polygon'
-
object.distance(other)—— 返回该几何对象到其他几何对象的最小距离(浮点类型)。
1>>> Point(0,0).distance(Point(1,1))
21.4142135623730951
-
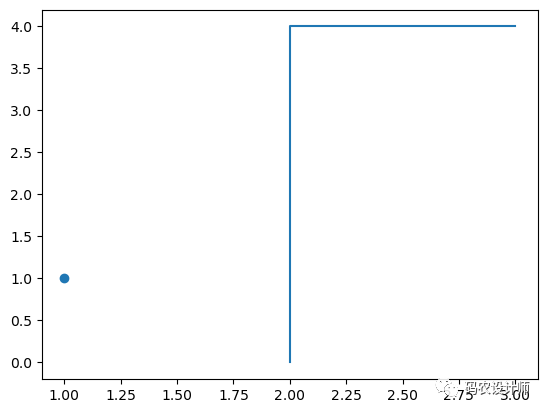
object.hausdorff_distance(other)—— 返回该几何对象到另一个几何对象的Hausdorff距离(浮点数)。两个几何对象之间的Hausdorff距离(豪斯多夫距离,集合之间的距离度量)是任何一个几何对象上的一个点与另一个几何对象上的最近点之间的最远距离。
1>>> point = Point(1, 1)
2>>> line = LineString([(2, 0), (2, 4), (3, 4)])
3
4>>> point.hausdorff_distance(line)
53.605551275463989
6
7>>> point.distance(Point(3, 4))
83.605551275463989
上述点、线之间的关系如下图所示:
-
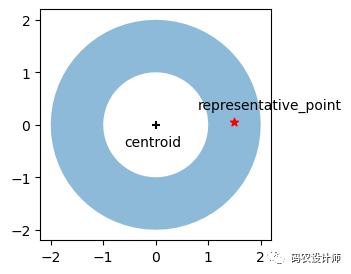
object.representative_point()—— 返回一个在几何对象内的点。该点为标记点,在计算时依照计算量最小而定,至确保在几何对象内部,并不代表几何对象的质心。
1>>> donut = Point(0, 0).buffer(2.0).difference(Point(0, 0).buffer(1.0))
2>>> donut
3<POLYGON ((1.99 -0.196, 1.962 -0.39, 1.914 -0.581, 1.848 -0.765, 1.764 -0.94...>
4
5# 几何对象的质心
6>>> donut.centroid
7<POINT (0 0)>
8
9>>> donut.representative_point()
10<POINT (1.498 0.049)>
两点与原几何对象的关系如下图所示:

END

本篇文章来源于微信公众号: 码农设计师
