本系列文章是根据Shapely官方文档翻译整理,学习任何一个Python第三方库,其官方文档都是最好的学习资料。相比网络搜索得到的一些资料,官方文档是权威的一手资料,其内容全面、准确可靠。通过官方文档入手,能够保证学习认知不会有大偏差。在学习完官方文档后,可以在寻找其他资料进一步学习。
点击“阅读原文”或者直接访问下方链接,查看翻译整理的“Shapely 2.0.0 中文文档”。
https://www.mizhushare.com/docs/shapely-2-0-0-%e4%b8%ad%e6%96%87%e6%96%87%e6%a1%a3/-
可以通过百度网盘获取,需要在本地配置代码运行环境:
链接:https://pan.baidu.com/s/1iWGGhB4kra9V7bUj-CWR0w?pwd=mnsj提取码:mnsj
-
前往GitHub详情页面,单击 code 按钮,选择Download ZIP选项:
https://github.com/returu/ShapelyTrue 或 False。其中,一元谓词作为只读属性实现。
-
object.has_z :
如果几何要素不仅有x和y,而且还有z坐标,则返回True。
1>>> Point(0, 0).has_z
2False
3
4>>> Point(0, 0, 0).has_z
5True
-
bject.is_ccw:
如果坐标按逆时针顺序排列,则返回True(以正面标记的面积来框定区域)。该方法只适用于LinearRing对象。
1>>> LinearRing([(1,0), (1,1), (0,0)]).is_ccw
2True
非预期方向的环可以通过以下代码进行翻转操作:
1>>> ring = LinearRing([(0,0), (1,1), (1,0)])
2>>> ring.is_ccw
3False
4
5# 将坐标序列反向排列
6>>> ring2 = LinearRing(list(ring.coords)[::-1])
7>>> ring2.is_ccw
8True
-
object.is_empty:
如果要素的内部和边界为空集,则返回True。
1>>> Point().is_empty
2True
3
4>>> Point(0, 0).is_empty
5False
使用python内置模块operator中的attrgetter()函数,一元谓词is_empty 能够用作python内置函数filter()的谓词,来对列表中的对象进行批量判断和过滤。
1>>> from operator import attrgetter
2
3>>> empties = filter(attrgetter('is_empty'), [Point(), Point(0, 0)])
4
5>>> list(empties)
6[<POINT EMPTY>]
-
object.is_ring:
如果要素是一个闭合的、简单的LineString,返回True。一个封闭的要素的边界与空集重合。该属性适用于LineString和LinearRing实例,但对其他实例无意义。
1>>> LineString([(0, 0), (1, 1), (1, -1)])
2<LINESTRING (0 0, 1 1, 1 -1)>
3>>> LineString([(0, 0), (1, 1), (1, -1)]).is_ring
4False
5
6>>> LinearRing([(0, 0), (1, 1), (1, -1)])
7<LINEARRING (0 0, 1 1, 1 -1, 0 0)>
8>>> LinearRing([(0, 0), (1, 1), (1, -1)]).is_ring
9True
-
object.is_simple:
如果该要素不自相交,则返回True。该属性只对LineString和LinearRing有意义。
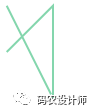
1>>> LineString([(0, 0), (1, 1), (1, -1), (0, 1)])
2<LINESTRING (0 0, 1 1, 1 -1, 0 1)>
3’
4>>> LineString([(0, 0), (1, 1), (1, -1), (0, 1)]).is_simple
5False
上述几何对象如下图所示:
-
object.is_valid:
如果要素是”有效 “的,则返回True。
有效性测试只对多边形Polygons 和复合多边形MultiPolygons有意义。对于其他类型的几何要素,总是返回True。
一个有效的多边形Polygon 不得拥有任何重叠的外部或内部环;一个有效的复合多边形MultiPolygon不会与任何多边形重叠。对无效要素进行的操作可能会失败。
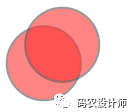
1>>> Polygons = MultiPolygon([Point(0, 0).buffer(2.0), Point(1, 1).buffer(2.0)]) # buffer()--缓冲操作
2>>> Polygons
3<MULTIPOLYGON (((2 0, 1.99 -0.196, 1.962 -0.39, 1.914 -0.581, 1.848 -0.765, ...>
4
5>>> Polygons.is_valid
6False
上述几何对象如下图所示:
is_valid谓词可以用来编写一个验证装饰器,可以确保只有有效的对象从构造函数返回。
1# 标准库 functools 中的 wrap 函数用于包装函数, 不改变原有函数的功能, 仅改变原有函数的一些属性, 例如 __name__, __doc__, __annotations__ 等属性
2>>> from functools import wraps
3>>> from shapely.errors import TopologicalError
4
5>>> def validate(func):
6... @wraps(func)
7... def wrapper(*args , **kwargs):
8... ob = func(*args , **kwargs)
9... if not ob.is_valid:
10... raise TopologicalError("给出的参数不能确定一个有效的几何对象!")
11... return ob
12... return wrapper
13...
14
15>>> @validate
16... def ring(coordinates):
17... return LinearRing(coordinates)
首先创建一个“无效”的几何对象:
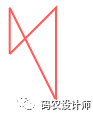
1>>> coords = [(0, 0), (1, 1), (1, -1), (0, 1)]
2>>> LinearRing(coords)
3<LINEARRING (0 0, 1 1, 1 -1, 0 1, 0 0)>
4>>> ring(coords)
5Traceback (most recent call last):
6 File "<stdin>", line 1, in <module>
7 File "<stdin>", line 6, in wrapper
8shapely.errors.TopologicalError: 给出的参数不能确定一个有效的几何对象!
再创建一个“有效”的几何对象:
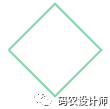
1>>> coords2 = [(0, 0), (1, 1), (2, 0), (1, -1)]
2>>> ring(coords2)
3<LINEARRING (0 0, 1 1, 2 0, 1 -1, 0 0)>

END

本篇文章来源于微信公众号: 码农设计师
