本系列文章是根据Shapely官方文档翻译整理,学习任何一个Python第三方库,其官方文档都是最好的学习资料。相比网络搜索得到的一些资料,官方文档是权威的一手资料,其内容全面、准确可靠。通过官方文档入手,能够保证学习认知不会有大偏差。在学习完官方文档后,可以在寻找其他资料进一步学习。
点击“阅读原文”或者直接访问下方链接,查看翻译整理的“Shapely 2.0.0 中文文档”。
https://www.mizhushare.com/docs/shapely-2-0-0-%e4%b8%ad%e6%96%87%e6%96%87%e6%a1%a3/-
可以通过百度网盘获取,需要在本地配置代码运行环境:
链接:https://pan.baidu.com/s/1iWGGhB4kra9V7bUj-CWR0w?pwd=mnsj提取码:mnsj
-
前往GitHub详情页面,单击 code 按钮,选择Download ZIP选项:
https://github.com/returu/ShapelyShapely还提供了构建新几何对象的空间分析方法。这些方法将总是返回一个新的几何对象。例如,一个不相交的几何体的交集将返回一个空的GeometryCollection,而不是None或False。要测试一个非空的结果,请使用几何对象的is_empty属性。
-
object.boundary:
按集合论,返回一个代表该对象边界的更低一维的几何对象。即,多边形的边界是一条线,一条线的边界是一系列点的集合。一个点的边界是一个空集。
1>>> coords = [((0, 0), (1, 1)), ((-1, 0), (1, 0))]
2>>> lines = MultiLineString(coords)
3>>> lines
4<MULTILINESTRING ((0 0, 1 1), (-1 0, 1 0))>
5
6>>> lines.boundary
7<MULTIPOINT (-1 0, 0 0, 1 0, 1 1)>
8
9>>> list(lines.boundary.geoms)
10[<POINT (-1 0)>, <POINT (0 0)>, <POINT (1 0)>, <POINT (1 1)>]
11
12>>> print(lines.boundary.boundary)
13GEOMETRYCOLLECTION EMPTY
-
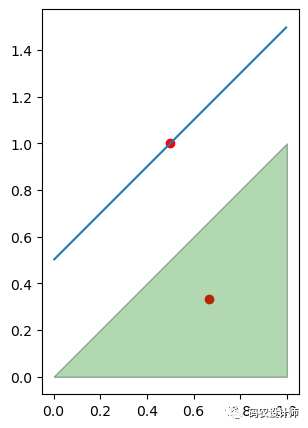
object.centroid:
返回几何对象的几何中心点,即质心。
一个对象的质心可能是组成它的一个点,但这并不是必然的。
1# 线要素
2>>> line = LineString([(0, 0.5), (1, 1.5)])
3>>> print(line.centroid)
4POINT (0.5 1)
5
6# 面要素
7>>> polygon = Polygon([(0, 0), (1, 1), (1, 0)])
8>>> print(polygon.centroid)
9POINT (0.6666666666666666 0.3333333333333333)
其关系图如下所示:
-
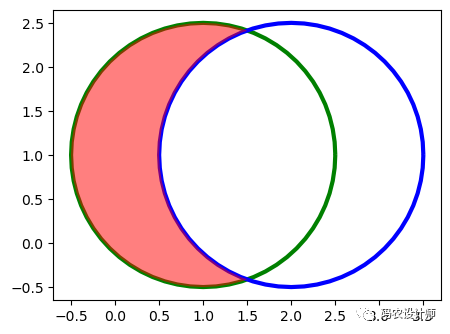
object.difference(other):
返回构成该几何对象的且不构成另一个对象的点的集合。即,相减操作。
difference 操作只适用于二维对象,不能用在低维对象上(例如线和点要素),在这些情况下,difference 方法返回一个名为self的对象的副本。
1# buffer()为缓冲区操作
2>>> a = Point(1, 1).buffer(1.5)
3>>> b = Point(2, 1).buffer(1.5)
4
5>>> result = a.difference(b)
6>>> result
7<POLYGON ((1.435 -0.435, 1.293 -0.471, 1.147 -0.493, 1 -0.5, 0.853 -0.493, 0...>
结果如下图所示(绿色圆为几何对象a,蓝色圆为几何对象b,红色填充部分为返回结果):
-
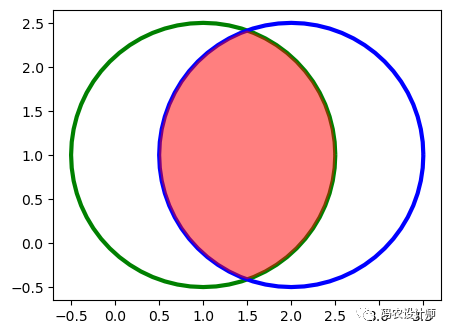
object.intersection(other):
返回该对象与另一个几何对象的交集。即,相交操作。
1>>> a = Point(1, 1).buffer(1.5)
2>>> b = Point(2, 1).buffer(1.5)
3
4>>> result = a.intersection(b)
5>>> result
6<POLYGON ((2.493 0.853, 2.471 0.707, 2.435 0.565, 2.386 0.426, 2.323 0.293, ...>
结果如下图所示(绿色圆为几何对象a,蓝色圆为几何对象b,红色填充部分为返回结果):
-
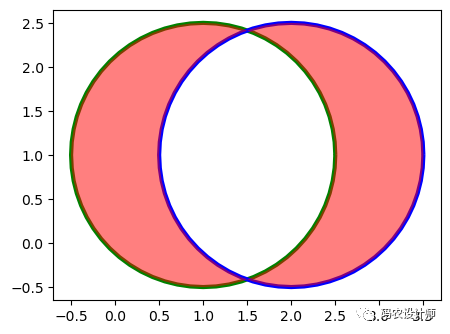
object.symmetric_difference(other):
返回这个对象中不在另一个几何对象中的点的表示,以及另一个对象中不在这个几何对象中的点的表示。即,对称差操作。
1>>> a = Point(1, 1).buffer(1.5)
2>>> b = Point(2, 1).buffer(1.5)
3
4>>> result = a.symmetric_difference(b)
5>>> result
6<MULTIPOLYGON (((1.574 -0.386, 1.707 -0.323, 1.833 -0.247, 1.952 -0.16, 2.06...>
结果如下图所示(绿色圆为几何对象a,蓝色圆为几何对象b,红色填充部分为返回结果):
-
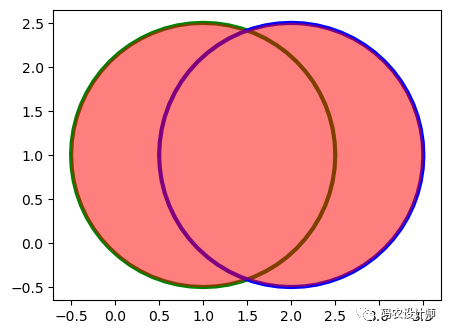
object.union(other):
返回该对象和另一个几何对象的点集的合集。即,合并操作。
返回的对象类型取决于运算对象之间的关系。例如,多边形的合并将是一个多边形或一个复合多边形,这取决于它们是否相交。
1>>> a = Point(1, 1).buffer(1.5)
2>>> b = Point(2, 1).buffer(1.5)
3
4>>> result = a.union(b)
5>>> result
6<POLYGON ((1.435 -0.435, 1.293 -0.471, 1.147 -0.493, 1 -0.5, 0.853 -0.493, 0...>
结果如下图所示(绿色圆为几何对象a,蓝色圆为几何对象b,红色填充部分为返回结果):
合并操作的语义因几何对象的类型而异。例如,比较多边形合并之后的边界(LineString类型)和它们的边界的合并结果(MultiLineString类型)。
1# 多边形合并之后的边界
2>>> a.union(b).boundary
3<LINESTRING (1.435 -0.435, 1.293 -0.471, 1.147 -0.493, 1 -0.5, 0.853 -0.493,...>
4>>> a.union(b).boundary.geom_type
5'LineString'
6
7# 边界的合并结果
8>>> a.boundary.union(b.boundary)
9<MULTILINESTRING ((2.5 1, 2.493 0.853, 2.471 0.707, 2.435 0.565, 2.386 0.426...>
10>>> a.boundary.union(b.boundary).geom_type
11'MultiLineString'
对于较多对象的合并操作,union()需要较多计算资源。建议使用更高效的shapely.ops.unary_union()方法。
-
上述集合论的方法也可以通过运算符来调用:
1>>> from shapely import wkt
2
3>>> p1 = wkt.loads('POLYGON((0 0,1 0,1 1,0 1,0 0))')
4>>> p2 = wkt.loads('POLYGON((0.5 0, 1.5 0, 1.5 1, 0.5 1, 0.5 0))')
5
6# intersection
7>>> p1 & p2
8<POLYGON ((0.5 0, 0.5 1, 1 1, 1 0, 0.5 0))>
9
10# union
11>>> p1 | p2
12<POLYGON ((0 0, 0 1, 0.5 1, 1 1, 1.5 1, 1.5 0, 1 0, 0.5 0, 0 0))>
13
14# difference
15>>> p1 - p2
16<POLYGON ((0 0, 0 1, 0.5 1, 0.5 0, 0 0))>
17
18# symmetric_difference
19>>> p1 ^ p2
20<MULTIPOLYGON (((0 0, 0 1, 0.5 1, 0.5 0, 0 0)), ((1 1, 1.5 1, 1.5 0, 1 0, 1 ...>
21

END

本篇文章来源于微信公众号: 码农设计师
