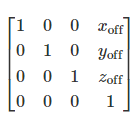A collection of affine transform functions are in the shapely.affinity module, which return transformed geometries by either directly supplying coefficients to an affine transformation matrix, or by using a specific, named transform (rotate, scale, etc.). The functions can be used with all geometry types (except GeometryCollection), and 3D types are either preserved or supported by 3D affine transformations.
shapely.affinity模块中有一组仿射变换函数,它们通过直接向仿射变换矩阵提供系数,或使用特定的、命名的变换(旋转、缩放等)来返回变换后的几何要素。这些函数可以用于所有的几何要素类型(GeometryCollection除外),而3D类型要么被保留,要么被3D仿射变换所支持。
New in version 1.2.17.
Returns a transformed geometry using an affine transformation matrix.
返回一个使用仿射变换矩阵变换后的几何对象。
The coefficient matrix is provided as a list or tuple with 6 or 12 items for 2D or 3D transformations, respectively.
系数矩阵以列表或元组的形式提供,对于二维或三维变换,分别有6或12项。
For 2D affine transformations, the 6 parameter matrix is:
对于二维仿射变换,6个参数矩阵为:
[a, b, d, e, xoff, yoff]
which represents the augmented matrix:
这代表了增强的矩阵:
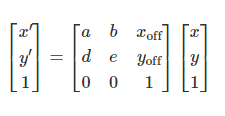
or the equations for the transformed coordinates:
或转换后的坐标方程:
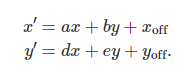
For 3D affine transformations, the 12 parameter matrix is:
对于三维仿射变换,12个参数矩阵为:
[a, b, c, d, e, f, g, h, i, xoff, yoff, zoff]
which represents the augmented matrix:
这代表了增强的矩阵:
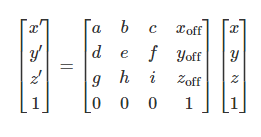
or the equations for the transformed coordinates:
或转换后的坐标方程:
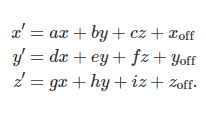
Returns a rotated geometry on a 2D plane.
返回一个二维平面上的旋转几何对象。
The angle of rotation can be specified in either degrees (default) or radians by setting use_radians=True. Positive angles are counter-clockwise and negative are clockwise rotations.
旋转的角度可以通过设置use_radians=True来指定度数(默认)或弧度。正的角度是逆时针旋转,负的是顺时针旋转。
The point of origin can be a keyword 'center' for the bounding box center (default), 'centroid' for the geometry’s centroid, a Point object or a coordinate tuple (x0, y0).
旋转原点可以是一个关键字’center’(表示中心)(默认),’centroid’(表示质心),一个点对象或一个坐标元组(x0, y0)。
The affine transformation matrix for 2D rotation with angle θ is:
角度为θ的二维旋转的仿射变换矩阵为:
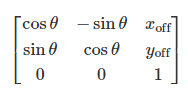
where the offsets are calculated from the origin (x0,y0):
其中偏移量是从原点(x0,y0)开始计算的:
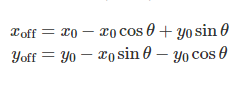
>>> from shapely import affinity
>>> line = LineString([(1, 3), (1, 1), (4, 1)])
>>> rotated_a = affinity.rotate(line, 90)
>>> rotated_b = affinity.rotate(line, 90, origin='centroid')(Source code, png, hires.png, pdf)
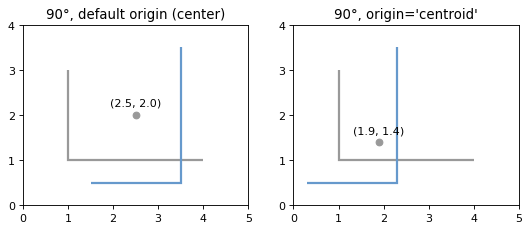
(gray) by an angle of 90° counter-clockwise (blue) using different origins.图16. 使用不同的旋转原点,将LineString(灰色)逆时针旋转90°(蓝色)。
Returns a scaled geometry, scaled by factors along each dimension.
返回一个按比例缩放的几何对象,沿每个维度都有相应的缩放系数。
The point of origin can be a keyword 'center' for the 2D bounding box center (default), 'centroid' for the geometry’s 2D centroid, a Point object or a coordinate tuple (x0, y0, z0).
缩放原点可以是一个关键字’center’(表示中心)(默认),’centroid’(表示质心),一个点对象或一个坐标元组(x0, y0)。
Negative scale factors will mirror or reflect coordinates.
负的比例系数将对坐标进行镜像操作。
The general 3D affine transformation matrix for scaling is:
用于缩放的一般三维仿射变换矩阵是:
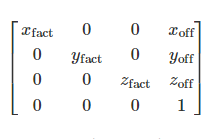
where the offsets are calculated from the origin (x0,y0,z0):
其中偏移量是从原点(x0,y0,z0)开始计算的:
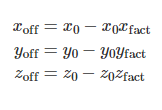
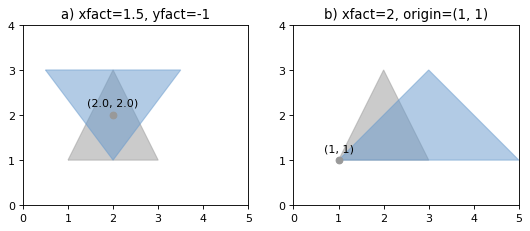
>>> triangle = Polygon([(1, 1), (2, 3), (3, 1)])
>>> triangle_a = affinity.scale(triangle, xfact=1.5, yfact=-1)
>>> triangle_a.exterior.coords[:]
[(0.5, 3.0), (2.0, 1.0), (3.5, 3.0), (0.5, 3.0)]
>>> triangle_b = affinity.scale(triangle, xfact=2, origin=(1,1))
>>> triangle_b.exterior.coords[:]
[(1.0, 1.0), (3.0, 3.0), (5.0, 1.0), (1.0, 1.0)](Source code, png, hires.png, pdf)
Returns a skewed geometry, sheared by angles along x and y dimensions.
返回一个沿x和y维度设定的角度进行扭曲操作的几何对象。
The shear angle can be specified in either degrees (default) or radians by setting use_radians=True.
扭曲角度可以用度数(默认)或者通过设置use_radians=True来指定弧度。
The point of origin can be a keyword 'center' for the bounding box center (default), 'centroid' for the geometry’s centroid, a Point object or a coordinate tuple (x0, y0).
扭曲原点可以是一个关键字’center’(表示中心)(默认),’centroid’(表示质心),一个点对象或一个坐标元组(x0, y0)。
The general 2D affine transformation matrix for skewing is:
一般二维仿射变换矩阵为:

where the offsets are calculated from the origin (x0,y0):
其中偏移量是从原点(x0,y0)开始计算的:
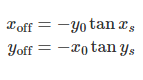
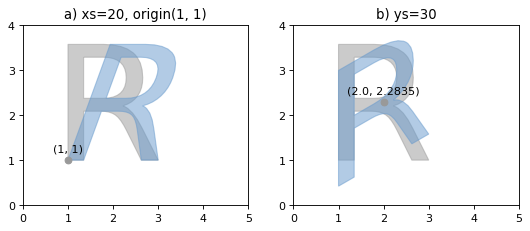
(Source code, png, hires.png, pdf)
Returns a translated geometry shifted by offsets along each dimension.
返回一个沿各维度平移的几何对象。
The general 3D affine transformation matrix for translation is:
用于平移的一般三维仿射变换矩阵为: