本系列配套练习数据下载链接:
链接:https://pan.baidu.com/s/1imKDcw9wZWk_ItR8fwugZw?pwd=mnsj提取码:mnsj
分析模式工具集能够提供对宏观空间模式进行量化的统计数据。这意味着,通过这些工具,可以将地理空间中的模式或趋势(例如,空间聚类的存在与否以及聚类程度的动态变化等)转换为具体的数值或指标,从而更客观地理解和分析这些数据。
分析模式工具集包含平均最近邻、高/低聚类、增量空间自相关、多距离空间聚类分析(Ripley’s K 函数)、空间自相关(Morans I)五个工具。
本次主要介绍平均最近邻工具。
-
1、概念:
平均最近邻工具用于测量每个要素的质心与其最近邻要素的质心之间的距离,并计算所有这些最近邻距离的平均值。
该工具不仅计算平均观测距离,还会计算预期平均距离,即假设随机分布(使用相同数量的要素覆盖相同的总面积)中的平均距离。通过比较这两个距离值,可以得到一个最近邻指数,该指数反映了要素的分布模式是聚类还是扩散。
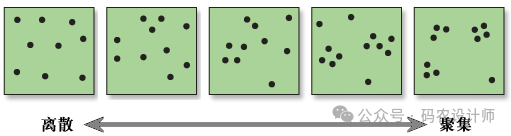
如果该平均距离小于假设随机分布中的平均距离,则会将所分析的要素分布视为聚类要素。如果该平均距离大于假设随机分布中的平均距离,则会将要素视为分散要素。平均最近邻比率通过观测的平均距离除以期望的平均距离计算得出。
该工具最适用于事件、事件点或其他定点要素数据,但也可用于处理线要素和面要素,此时会在计算中使用每个要素真正的几何质心。对于多点、折线 (polyline) 或由多部件组成的面,使用所有要素部件的加权平均中心来计算质心。点要素的加权项是 1,线要素的加权项是长度,而面要素的加权项是面积。
—————-
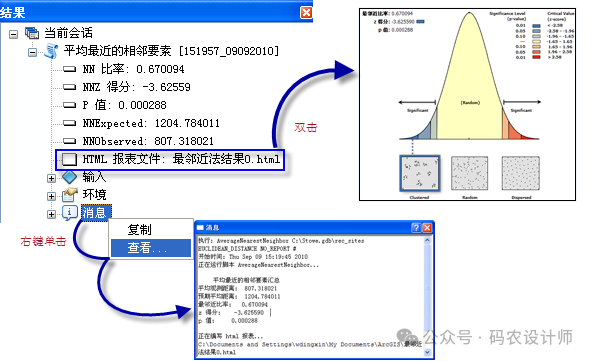
“平均最近邻”工具将返回五个值:
-
平均观测距离:每个要素与其最近邻要素之间的平均距离;
-
预期平均距离:假设随机分布中的平均距离;
-
最近邻指数:是“平均观测距离”与“预期平均距离”的比值。如果指数小于 1,所表现的模式为聚类;如果指数大于 1,则所表现的模式趋向于离散或竞争;
-
z 得分:统计显著性的量度,用来判断是否拒绝零假设。表示观测到的平均最近邻距离与期望的平均最近邻距离之间的标准偏差倍数。如果z得分为正且较高,这通常意味着观测到的要素之间的距离大于随机分布中的期望距离,即要素可能趋向于分散。相反,如果z得分为负且较低,这表示观测到的要素之间的距离小于期望的随机距离,即要素可能聚集在一起。
-
p 值:统计显著性的量度,用来判断是否拒绝零假设。用于检验观测到的空间模式是否具有统计显著性的概率值。在平均最近邻分析的上下文中,p值表示在完全随机的空间分布下,观测到与当前数据集相同或更极端的空间模式的概率。通常,如果p值小于预设的显著性水平(如0.05或0.01),我们可以拒绝空间分布是随机的这一假设,并认为观测到的空间模式是具有统计显著性的。
—————-
另外,在一些特殊情况下,输入要素可能会造成无效(面积为零)的最小外接矩形。在这种情况下,将使用基于输入要素的 XY 容差得到的一个较小值来创建最小外接矩形。例如,如果所有的要素都重合(也就是说,所有要素拥有完全相同的 X 和 Y 坐标),则在计算中将使用单一位置周围的一个非常小的方形面的面积。另一个例子是,所有要素完全对齐(例如,一条直线上的 3 个点);在这种情况下,将在计算中使用要素周围一个宽度很小的矩形面的面积。
该工具有以下适用的研究场景:
-
评估竞争或领地:量化并比较固定研究区域中的多种植物种类或动物种类的空间分布;比较城市中不同类型的企业的平均最近邻距离。 -
监视随时间变化的更改:评估固定研究区域中一种类型的企业的空间聚类中随时间变化的更改。 -
将观测分布与控制分布进行比较:例如,在木材分析中,如果给定全部可收获木材的分布,则最好将已收获面积图案与可收获面积图案进行比较,以确定砍伐面积是否比期望面积更为聚类。
-
2、工具:

-
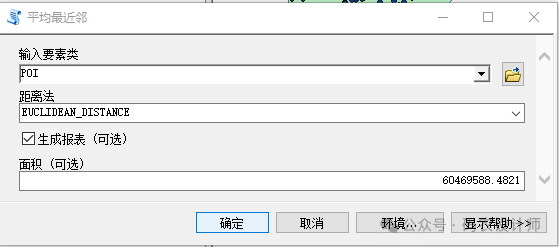
距离法:计算每个要素与邻近要素之间的距离的方式。EUCLIDEAN_DISTANCE(欧式距离)计算两点间的直线距离,MANHATTAN_DISTANCE(曼哈顿距离)将沿垂直轴度量的两点间的距离(城市街区),计算方法是对两点的 x 和 y 坐标的差值(绝对值)求和。 -
生成报表:指定工具是否将创建结果的图形汇总。默认不创建图形汇总。选中时,图形汇总将以 HTML 文件形式创建。 -
面积:表示研究区域大小的数值。如果没有指定面积参数值,则使用输入要素周围最小外接矩形的面积。本次为面要素【区界】的面积值。
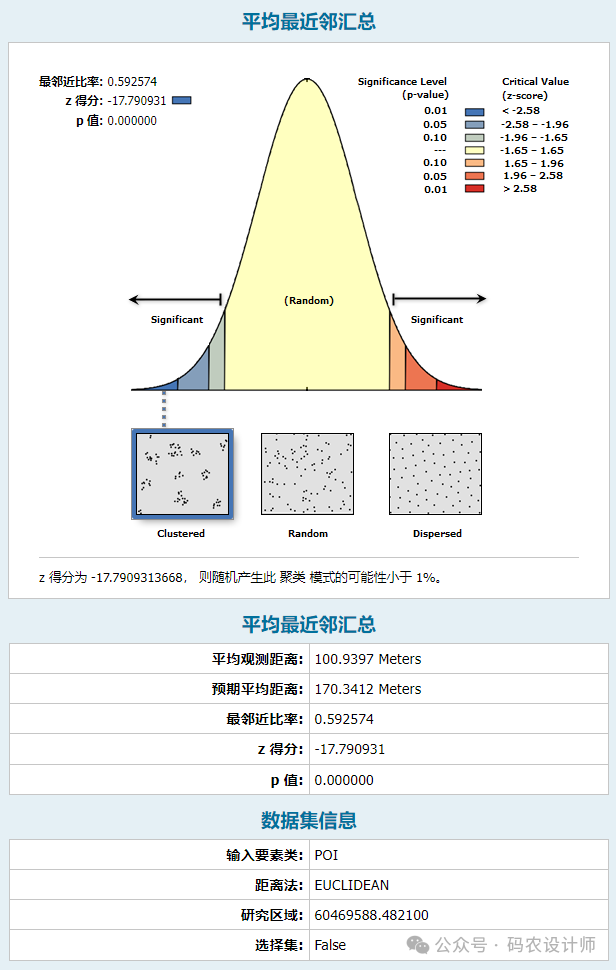
本次计算的最近邻指数约为0.59(小于1)、z 得分为-17.79,表示观测到的要素之间的距离小于期望的随机距离,因此点要素所表现的模式为聚类。同时,p值为0,标识观测到的空间模式是具有统计显著性的。


本篇文章来源于微信公众号: 码农设计师
