本系列配套练习数据下载链接:
链接:https://pan.baidu.com/s/1imKDcw9wZWk_ItR8fwugZw?pwd=mnsj提取码:mnsj
空间关系建模工具集可构建空间权重矩阵或利用回归分析建立空间关系模型,用于挖掘或量化要素间关系。
空间关系建模工具集包含地理加权回归、探索性回归、普通最小二乘法、生成网络空间权重、生成空间权重矩阵五个工具。
本次主要介绍普通最小二乘法 (OLS) 工具。
-
1、概念:
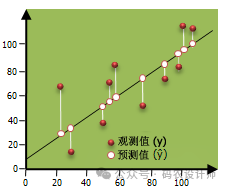
普通最小二乘法 (OLS) 工具用于执行全局“普通最小二乘法 (OLS)”线性回归可生成预测,也可为一个因变量针对它与一组解释变量关系建模。
—————-
使用OLS工具时,需要提供一个包含因变量和一组解释变量的数据集,OLS工具对因变量(希望预测或解释的变量)和解释变量(可能影响因变量的因素)有以下要求:
1、因变量的要求:
2、解释变量的要求:
-
线性关系:OLS回归假设因变量和解释变量之间存在线性关系。如果实际关系是非线性的,则需要对变量进行转换或选择其他适合的回归模型。
-
误差项的独立性:OLS回归假设误差项是独立的,即观测值之间的误差互不相关。如果误差项之间存在相关性,则违反了这一假设,可能导致模型的估计不准确。
-
误差项的正态性和同方差性:虽然这些假设在某些情况下可以放宽,但理想的OLS回归模型假设误差项服从正态分布,并且具有恒定的方差(同方差性)。
—————-
-
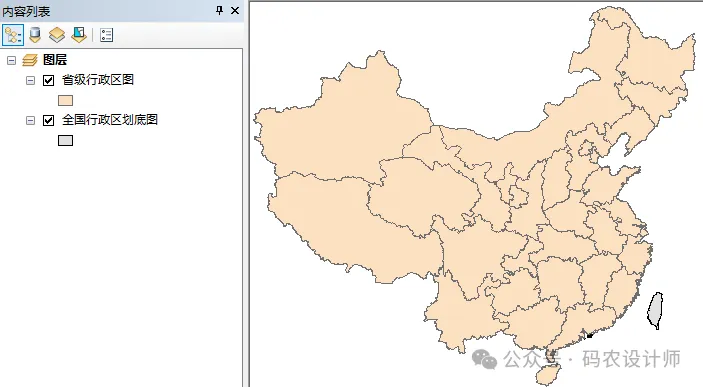
2、工具:
-
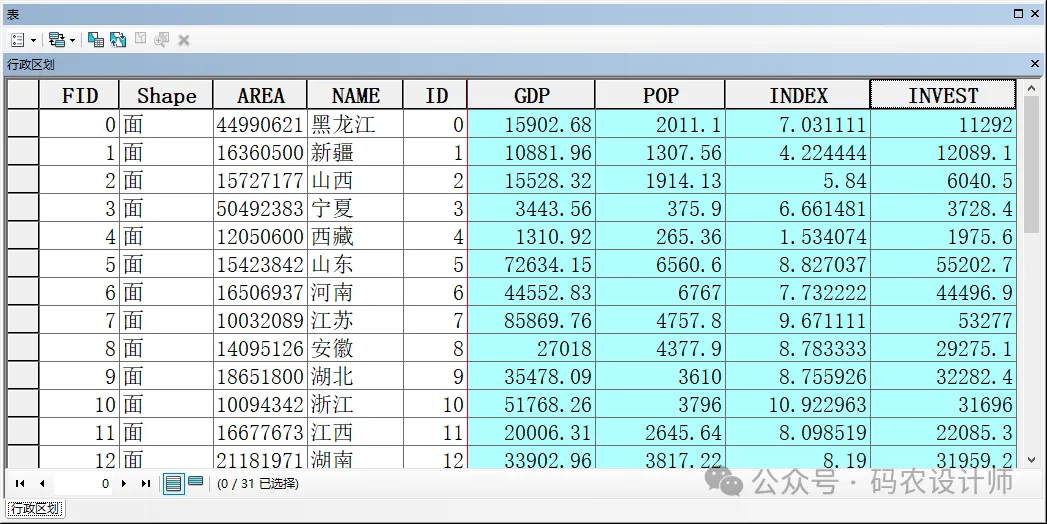
唯一 ID 字段:包含输入要素类中每个要素不同值的整型字段。该字段用于将模型预测连接到各个要素。因此,每个要素的 Unique ID 值都必须唯一,而且通常应是与要素类一同保留的永久性字段。FID/OID 字段无法直接用于唯一 ID 参数。 -
因变量设置为GDP字段; -
解释变量设置为年末就业人口、固定资产投资、市场化指数三个字段。
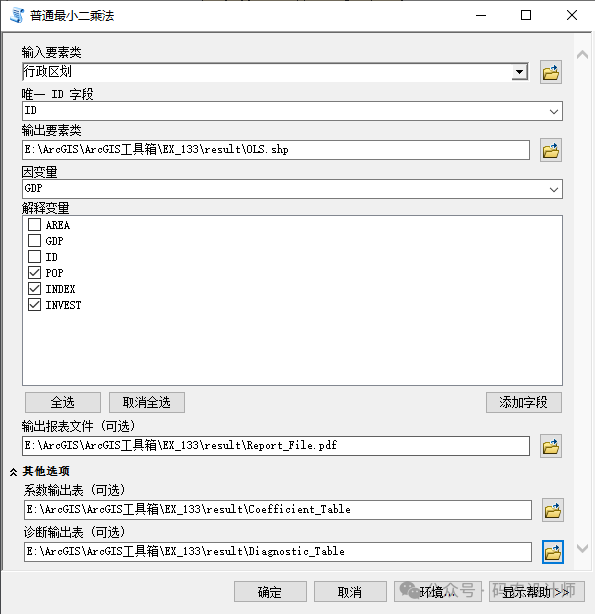
OLS 工具生成的输出包括以下几部分:
1、输出要素类:
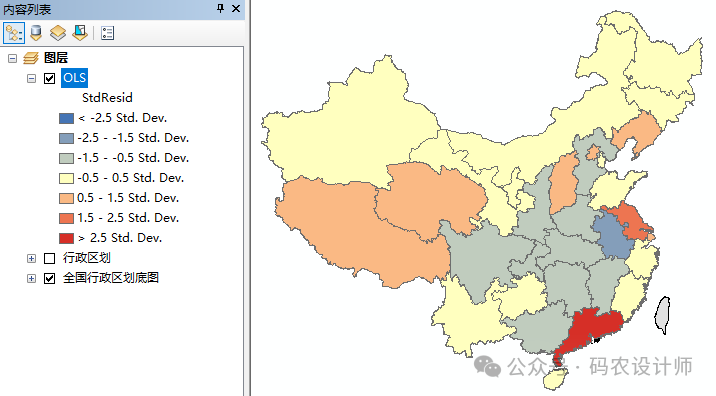
2、可选的 PDF 报表文件:
报表文件包含摘要报表中的所有信息以及附加图表,用于可帮助对模型进行评估。
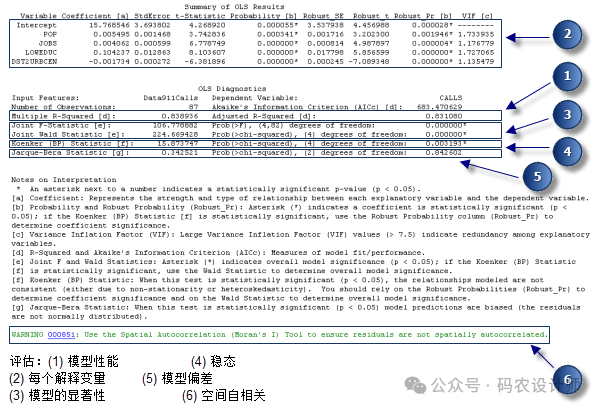
第一页提供与每个解释变量相关的信息,可使用该页中的信息来确定每个解释变量的系数是否具有统计显著性并带有预期符号 (+/-)。
-
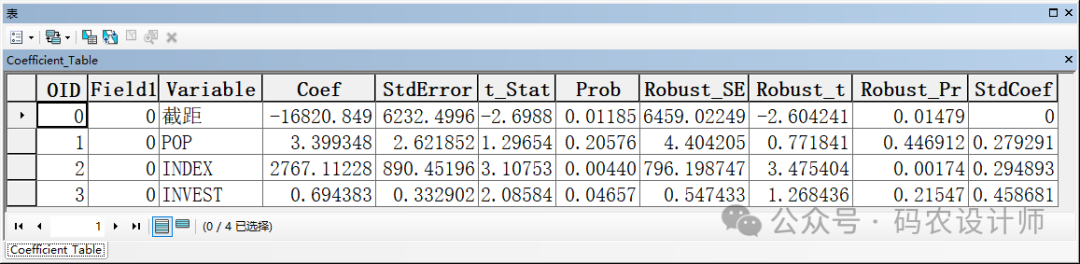
系数:每个解释变量的系数既反映它与因变量之间的关系强度,也反映它与因变量之间的关系类型。
-
概率或稳健概率(Robust_Pr):星号(*)表示系数具有统计学上的显著性(p < 0.01)。另外,如果Koenker(BP)统计量(在报表第二页)具有统计学上的显著性,则使用稳健概率列(Robust_Pr)来确定系数显著性。
-
VIF(方差膨胀因子):用于测量解释变量中的冗余(表示有问题的多重共线性)。一般来说,与大于 7.5 的 VIF 值关联的解释变量应逐一从回归模型中移除,直到剩下的所有解释变量的 VIF 值均小于 7.5。
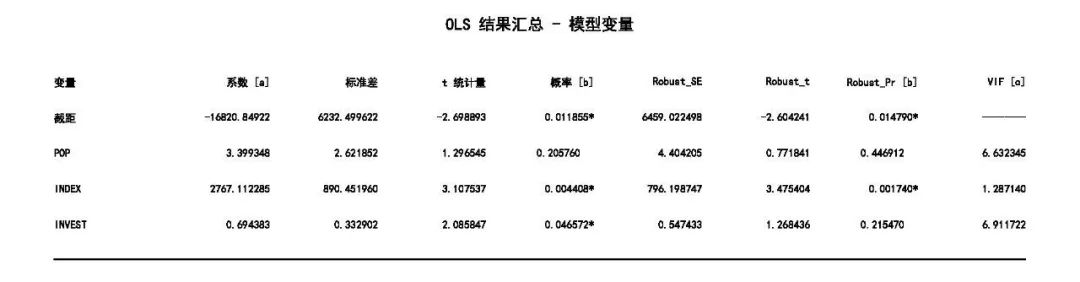
第二页列出了 OLS 诊断的检查结果以及说明每项检查的重要性原因的解释注意事项。
-
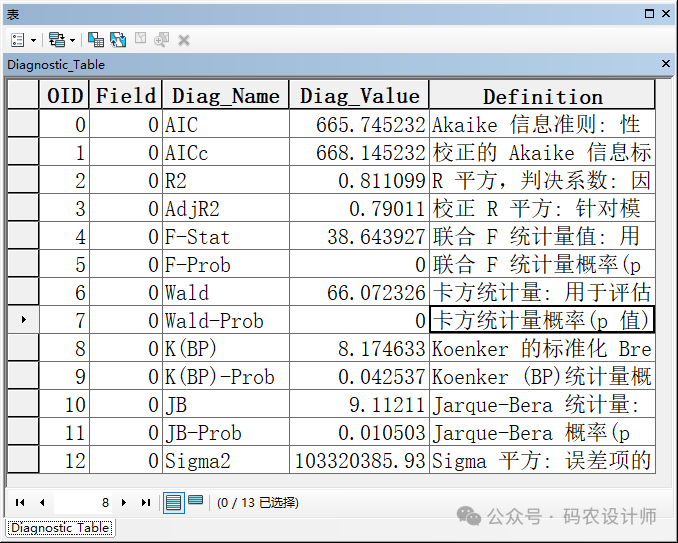
评估模型性能:多重可决系数Multiple R-Squared(R平方的倍数) 和校正可决系数Adjusted R-Squared(校正R平方) 的值都可用于测量模型的性能。值的可能范围从 0.0 到 1.0。由于“校正可决系数”的值与数据本身相关因而更能准确地衡量模型的性能,从而反映模型的复杂性(变量数),因此“校正可决系数”值通常要比“多重可决系数”值略小。如果“校正可决系数”的值为 0.50,则表示模型可解释因变量中大约 50% 的变化。
-
评估模型是否具有显著性:联合 F 统计量和联合卡方统计量均用于检验整个模型的统计显著性。只有在 Koenker (BP) 统计量不具有统计显著性时,“联合 F 统计量”才可信。如果 Koenker (BP) 统计量具有显著性,应参考“联合卡方统计量”来确定整个模型的显著性。这两种检验的零假设均为模型中的解释变量不起作用。对于大小为 95% 的置信度,p 值(概率)小于 0.05 表示模型具有统计显著性。
-
评估稳态:Koenker (BP) 统计量(Koenker 的标准化 Breusch-Pagan 统计量)是一种检验方法,用于确定模型的解释变量是否在地理空间和数据空间中都与因变量具有一致的关系。如果模型在地理空间中一致,由解释变量表示的空间进程在研究区(进程稳态)各位置处的行为也将一致。如果模型在数据空间中一致,则预测值与每个解释变量之间关系的变化不会随解释变量值的变化而变化(模型不存在异方差性)。假设要对犯罪情况进行预测,其中一个解释变量为收入。如果对收入的中位数较小的位置的预测比对收入的中位数较大的位置的预测更准确,则说明模型的异方差性就会出现问题。该检验的零假设为所检验的模型是稳态的。对于大小为 95% 的置信度,p 值(概率)小于 0.05 表示模型具有统计学上的显著异方差性和/或非稳态。如果该检验的结果具有统计显著性,则需参考稳健系数标准差和概率来评估每个解释变量的效果。具有统计显著性非稳态的回归模型通常很适合进行地理加权回归 (GWR) 分析。
-
评估模型偏差:Jarque-Bera 统计量用于指示残差(已观测/已知的因变量值减去预测/估计值)是否呈正态分布。该检验的零假设为残差呈正态分布,因此,如果为这些残差建立直方图,这些残差的分布将与典型钟形曲线或高斯分布相似。当该检验的 p 值(概率)较小(例如,对于大小为 95% 的置信度,其值小于 0.05)时,回归不会呈正态分布,并指示您的模型有偏差。如果残差还存在统计学上显著的空间自相关,则偏差可能是模型指定错误的结果,比如,该模型的某个关键变量缺失、尝试构建非线性关系模型、数据的某些异常值存在影响或者存在很强的异方差性。

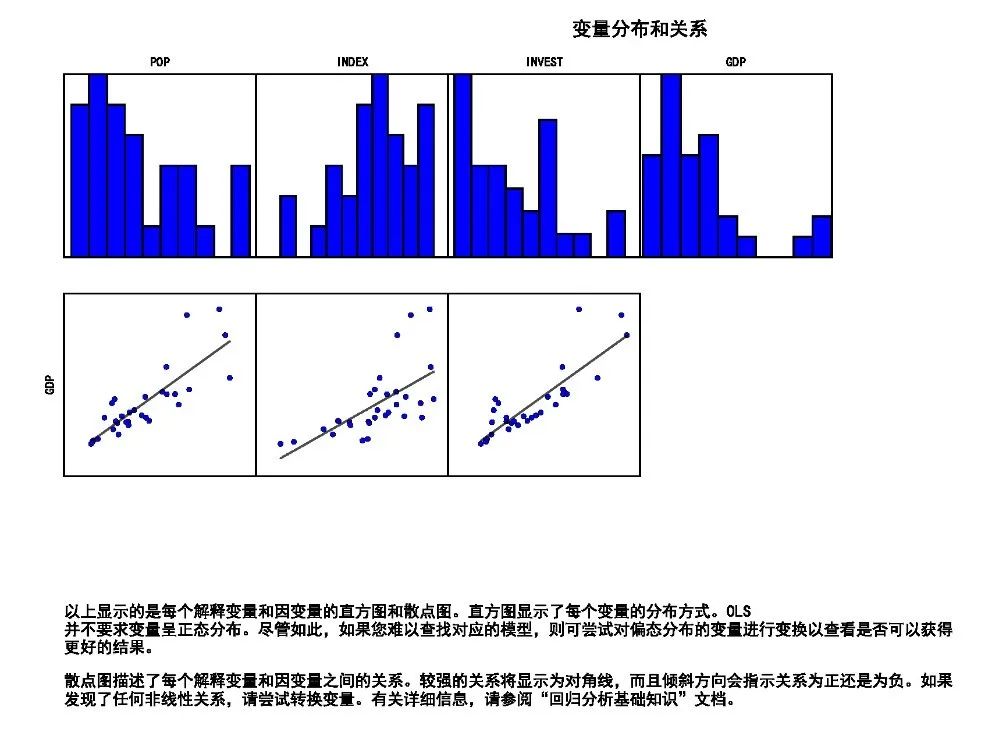
第三页显示模型中每个变量的分布直方图以及显示因变量与每个解释变量之间关系的散点图,散点图将显示哪些变量是最好的预测因子。这些散点图还可用于检查变量之间的非线性关系。。
如果模型存在偏差(通过具有统计显著性的 Jarque-Bera p 值指示),可查找直方图之间的偏分布,并尝试变换这些变量,以查看这是否可以消除偏差并改善模型性能。在某些情况下,变换一个或多个变量将修复非线性关系并消除模型偏差。
另外,数据中的异常值也可导致模型偏差。可查看直方图和散点图了解这些数据值和/或数据关系。
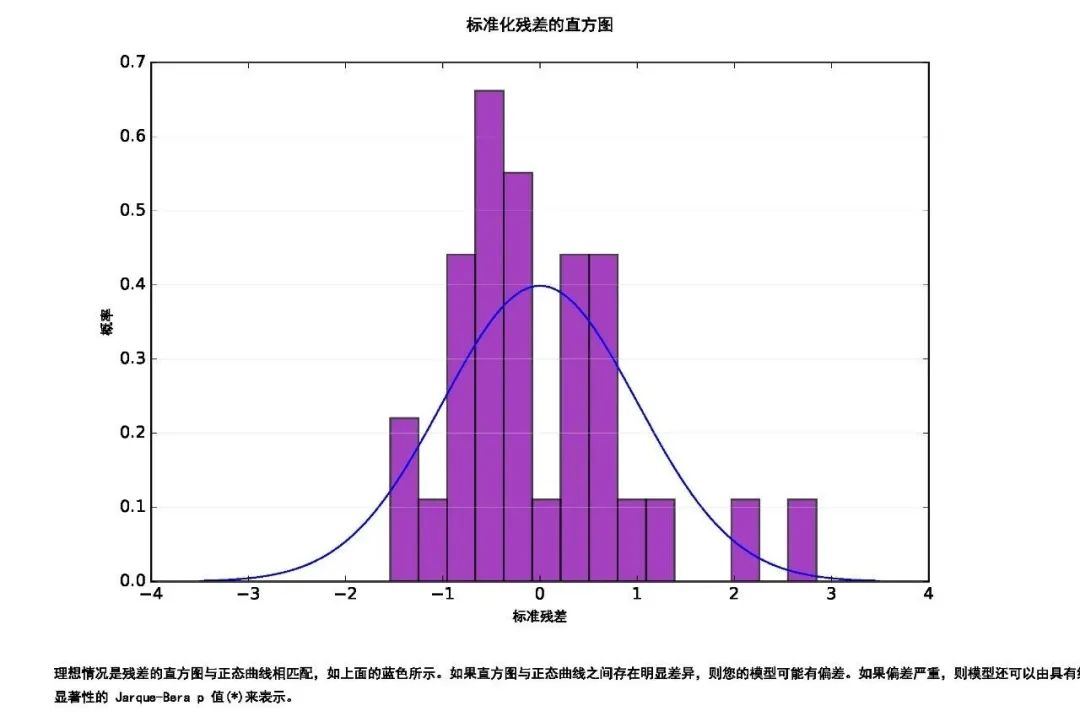
第四页显示模型偏高和偏低预计值的直方图。直方图的条块显示实际分布,如果残差实际上呈正态分布,则叠加在直方图顶部的蓝色线将显示直方图呈现的形状,因此需要检查 Jarque-Bera 检验以确定正态分布的偏差是否具有统计学上的显著性。
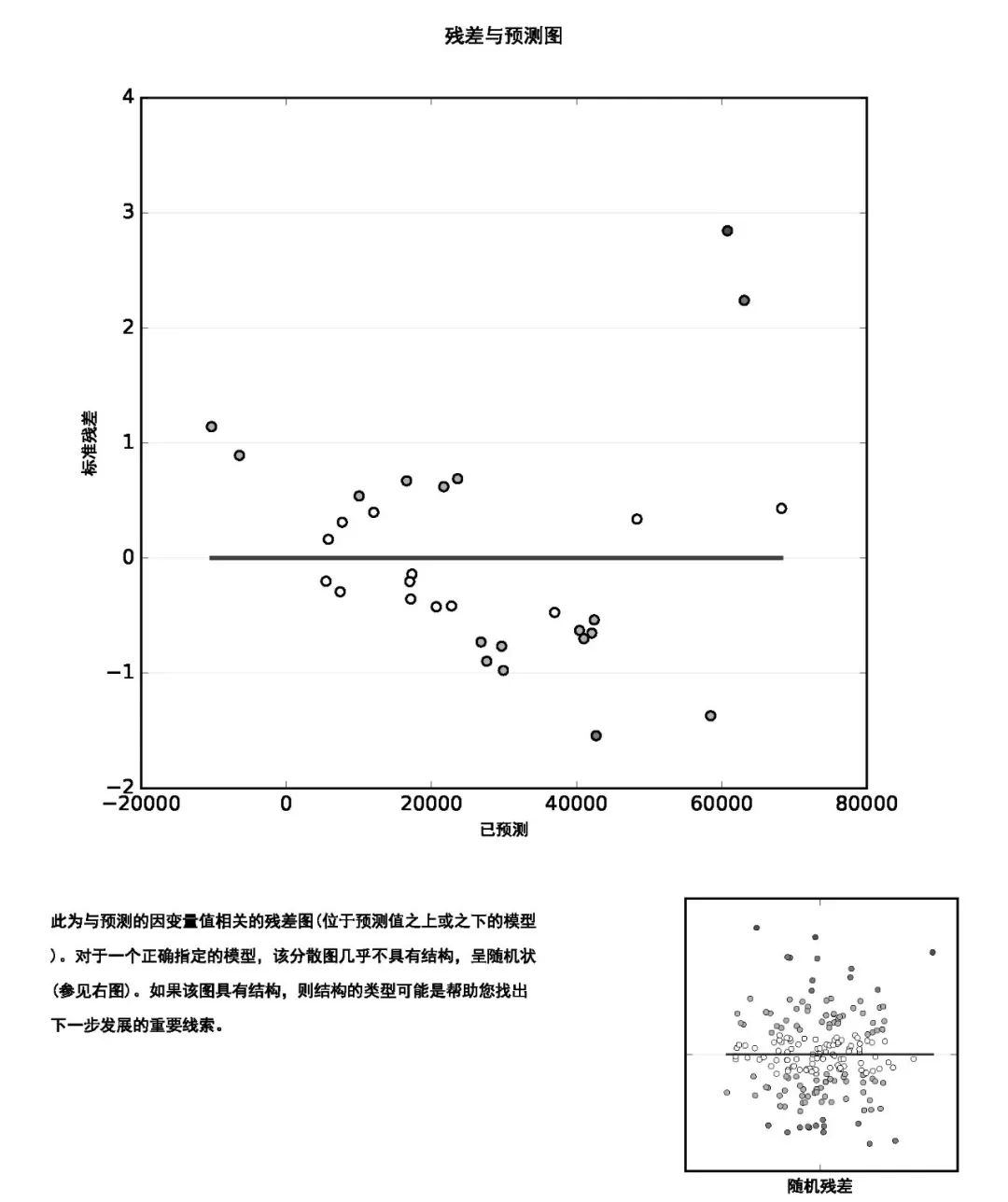
第五页显示描述模型残差与预测值之间关系的散点图,用于显示异方差性是否存在问题。
报表的最后一页记录创建报表时使用的所有参数设置。

3、可选解释变量系数表、可选回归诊断表:
在构建模型时,往往需要尝试不同的解释变量构建众多不同的模型,然后再进行对比选择,此时,可以使用 OLS 统计报告中的修正的 Akaike 信息准则 (AICc) 来比较不同的模型。AICc 值越小,模型就越好(换句话说,考虑到模型的复杂程度,具有越小 AICc 值的模型会更符合已观测的数据)。


本篇文章来源于微信公众号: 码农设计师
