本系列配套练习数据下载链接:
链接:https://pan.baidu.com/s/1imKDcw9wZWk_ItR8fwugZw?pwd=mnsj提取码:mnsj
-
1、概念:
地理加权回归 (GWR)工具是一种局部回归模型,允许模型的系数在空间上变化。
如果数据集中用于特定解释变量的值出现空间聚类,则很可能存在局部多重共线性问题。在全局回归模型中(如 OLS),当两个或更多变量具有多重共线性时,结果并不可靠。GWR 为数据集中的各要素构建局部回归方程来反映空间数据的非平稳性,这种方法特别适用于那些影响因素在空间上变化较大的情况。
-
核类型:
-
FIXED(固定核):这种核类型采用固定的距离或半径来确定每个位置的权重。也就是说,无论数据点的分布如何,核的形状和大小在空间中都是固定的。FIXED核类型适用于数据点在空间中分布相对均匀的情况。 -
ADAPTIVE(自适应核):与FIXED核不同,ADAPTIVE核会根据数据点的局部密度来调整核的大小和形状。在数据点密集的区域,核会变小,以便更好地捕捉局部的变化;而在数据点稀疏的区域,核会变大,以包含更多的信息。这种核类型适用于数据点在空间中分布不均的情况。
-
带宽方法:
-
AICc:AICc代表“赤池信息准则校正版”(Akaike Information Criterion with a correction)。AIC准则是衡量模型拟合优良性的一种标准,它考虑了模型的复杂度与模型拟合之间的平衡。AICc是AIC的一个修正版,特别适用于小样本情况。在GWR中,选择AICc作为带宽方法意味着工具会自动寻找那个使模型复杂度与拟合效果达到最优平衡的带宽值。AICc值越小,表明模型的质量越好,既不过于复杂也不过于简单。 -
CV:CV代表交叉验证(Cross-Validation)。在这种方法中,模型会对每一个数据点进行逐一排除,并使用剩余的数据来预测被排除点的值。通过这种方法,可以评估模型在未见数据上的预测性能。在GWR中,选择CV作为带宽方法时,工具会选择那个使得交叉验证误差最小的带宽,即模型在预测新数据时表现最好的带宽。 -
BANDWIDTH_PARAMETER:该选项允许用户直接指定一个带宽值或相邻点的数目,而不是通过优化准则(如AICc或CV)来自动选择。当对自己的数据和模型有深入了解,或者想要根据特定的研究需求来设定带宽时,可以选择这个选项。通过直接指定带宽,可以更精确地控制模型的局部性,但这也需要更多的专业知识和经验。

—————-
-
输出要素类 -
可选系数栅格表面 -
显示模型变量和诊断结果的辅助表 -
预测输出要素类
-
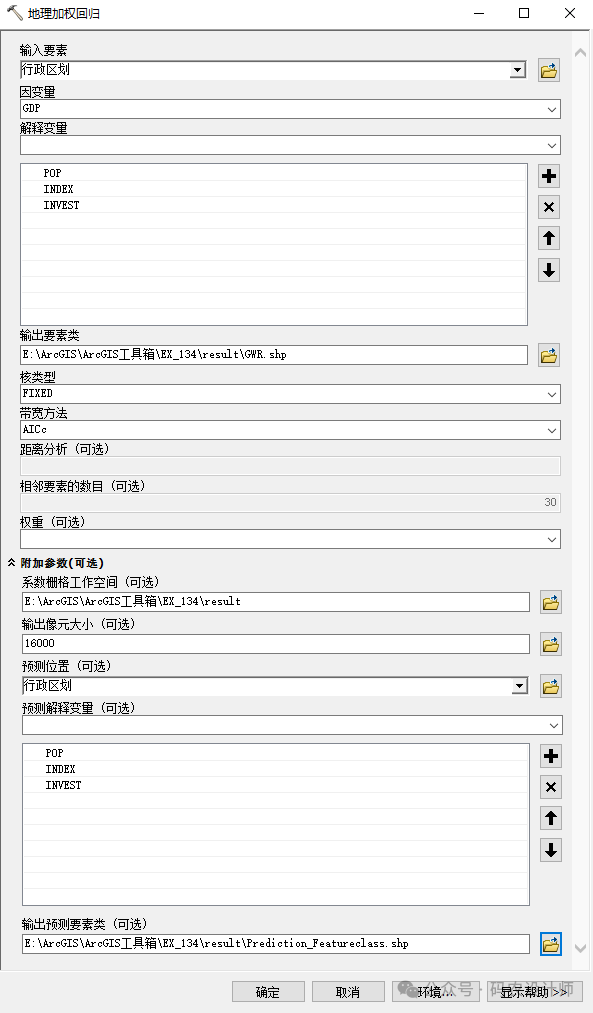
2、工具:
-
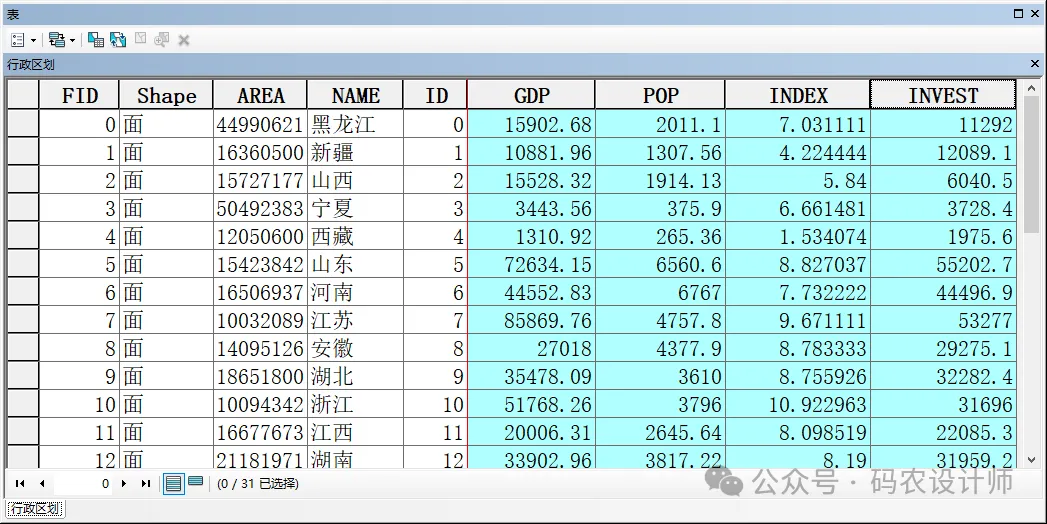
因变量和解释变量应该是包含各种值的数值型字段,并且应该包含一定的值范围。GWR不适于预测二进制结果(例如,因变量的所有值不是 1 就是 0)。如果数据中存在缺失值,可以在运行GWR工具之前使用填充缺失值工具进行处理。 -
权重:包含单个要素的空间权重的数值字段。此权重字段允许部分要素在模型校准过程中比其他要素更为重要。主要用于在不同位置采集的样本数目发生变化以及对因变量和自变量中的值求平均值的情况中,并且样本越多,位置越稳定。如果一个位置平均具有 25 个不同的样本,但其他位置平均只具有 2 个样本,则可将样本数用作权重字段,以便在模型校准中具有更多样本的位置比具有少量样本的位置有更大的影响力。
-
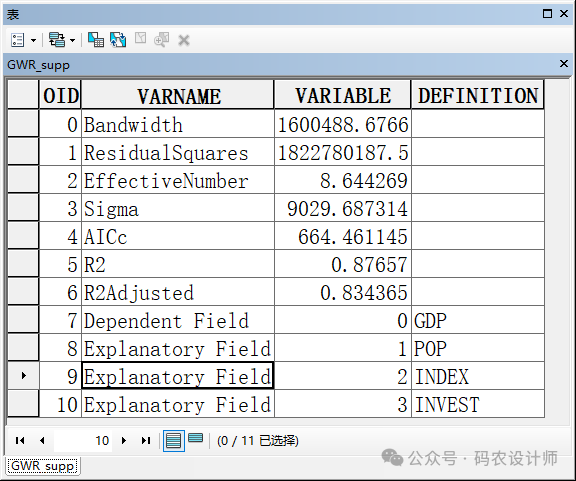
Bandwidth或Neighbors:是指用于各个局部估计的带宽或相邻点数目,控制模型中的平滑程度。 -
ResidualSquares:模型中的残差平方和(残差为观测所得 y 值与 GWR 模型所返回的 y 值估计值之间的差值)。该值越小,GWR模型拟合观测数据的效果越好。 -
EffectiveNumber:该值表示的是模型在每个位置上的有效参数数量,与带宽的选择有关(如果带宽设置得较大,那么会包含更多的邻近点,从而增加EffectiveNumber的值。反之亦然),可以看作是拟合值的方差与系数估计值的偏差之间的折衷表示。具体来说,EffectiveNumber反映了在特定带宽下,模型实际上使用了多少数据点来进行局部回归。由于GWR是一种局部回归技术,它会在每个位置根据邻近点的数据来估计模型参数。EffectiveNumber可以理解为在给定位置的局部回归中,有多少数据点“有效地”参与了模型的估计。EffectiveNumber可以作为评估GWR模型的一个重要指标,它可以帮助我们理解模型在不同空间位置上的稳定性和可靠性。一般来说,EffectiveNumber的值越高,表示在该位置的模型估计越稳定,因为更多的数据点被用来进行估计。然而,过高的EffectiveNumber值也可能意味着模型的局部性被削弱,因为过多的数据点被纳入了局部回归中。因此,在解释GWR结果时,需要综合考虑EffectiveNumber与其他统计指标(如R-squared、残差等)来评估模型的性能。 -
Sigma:该值为正规化剩余平方和(剩余平方和除以残差的有效自由度)的平方根。它是残差的估计标准差。此统计值越小越好。Sigma 用于 AICc 计算。 -
AICc:模型性能的一种度量,有助于比较不同的回归模型。考虑到模型复杂性,具有较低 AICc 值的模型将更好地拟合观测数据。AICc 不是拟合度的绝对度量,但对于比较适用于同一因变量且具有不同解释变量的模型非常有用。如果两个模型的 AICc 值相差大于 3,具有较低 AICc 值的模型将被视为更佳的模型。将 GWR AICc 值与 OLS AICc 值进行比较是评估从全局模型 (OLS) 移动到局部回归模型 (GWR) 的优势的一种方法。 -
R2:R 平方是拟合度的一种度量。其值在 0.0 到 1.0 范围内变化,值越大越好。该值可解释为回归模型所涵盖的因变量方差的比例。 -
R2Adjusted:校正的 R 平方值的计算将按分子和分母的自由度对R2进行正规化。这具有对模型中变量数进行补偿的效果,因此校正的 R2 值通常小于 R2 值。但是,执行此校正时,无法将该值的解释作为所解释方差的比例。在 GWR 中,自由度的有效值是带宽的函数,因此与像 OLS 之类的全局模型相比,校正程度可能非常明显。因此,AICc 是对模型进行比较的首选方式。
-
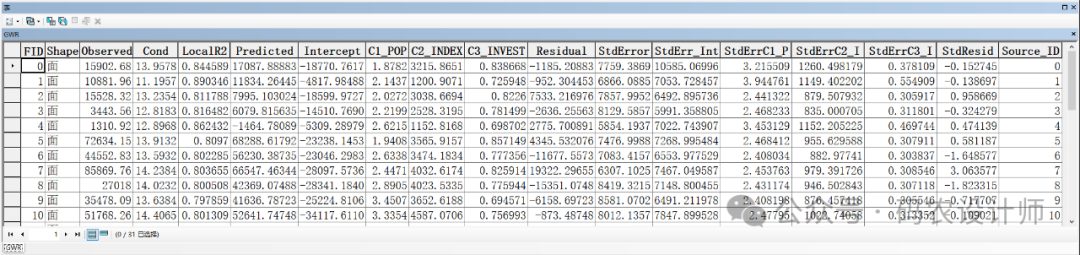
Cond:条件数,此诊断用于评估局部多重共线性。高的条件数可能意味着模型在该位置的预测可能不够稳定,因为解释变量之间可能存在较强的共线性(即变量之间高度相关)。条件数大于30的话,与之相关联的结果可能不可靠。 -
Local R2:局部R平方值(范围在0.0与1.0之间),用于衡量GWR模型在每个位置的拟合优度。该值越接近1,表示模型在该位置的预测值与观测值越接近,即模型的拟合效果越好。 -
Predicted:预测值,表示GWR模型在每个位置对因变量的预测结果。 -
Intercept:截距值,代表回归线在因变量轴上的截距。在GWR中,这个截距是随空间位置变化的。 -
C1/2/3:实际系数值,对于每个解释变量,GWR工具会生成一个与之对应的系数字段,这些字段通常命名为“C1_”、“C2_”,依此类推,具体编号取决于解释变量的顺序。系数值反映了各解释变量在不同空间位置上对因变量的局部影响程度。 -
Residual:残差,即观测值与模型预测值之间的差异。正值表示模型低估了实际值,负值则表示模型高估了实际值。
-
StdError:标准误差,表示模型预测值的标准偏差,用于衡量预测值的不确定性。 -
StdErr_Int:截距的标准误差,表示截距估计值的标准偏差,反映了截距估计的不确定性。 -
StdErrC1/2/3:系数标准误差,用于衡量每个系数估计值的可靠性。标准误差与实际系数值相比较小时,这些估计值的可信度会更高。较大标准误差可能表示局部多重共线性存在问题。 -
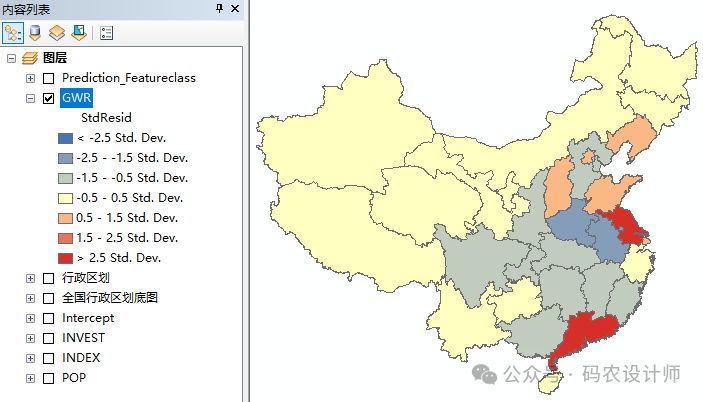
StdResid:标准化残差,是将残差除以其标准差得到的,用于评估残差是否异常大或异常小,从而判断模型是否适合数据。系统自动将生成的图层根据标准化残差进行了可视化渲染,此数值主要用来衡量每个参数系数的可靠性,一般来说,大于2.5倍标准差的地方可能会有些问题,例如下图中,江苏和广东两省的回归拟合效果不佳,其余省市拟合效果还比较理想。 -
Source_ID:原始数据集中每个观测点的唯一标识符,用于跟踪和识别每个观测点的来源。
|
|
|
|
|
通过就业人口回归系数图可以看出,就业人口对经济发展具有正向作用。劳动力作为新古典经济增长的重要因素,有利于经济增长。不过这种促进作用存在地区不均衡性,劳动力的经济贡献程度由南向北逐渐递减。南部地区作为我国人口迁移的活跃地区,其经济增长具有明显优势。 |
|
|
| 通过固定资产投资回归系数图可以看出,固定资产投资变化量对各省经济总量变化影响为正相关关系,其影响程度由东北向西南依次降低。高值区集中于环渤海和东北地区,低值区集中于南部省份。长期以来环渤海地区与东北地区经济发展侧重于资本密集型的重工业发展模式,而且国有企业比重大,故此对固定资产投资依赖程度深,经济结构单一性严重。而南方地区因其经济结构多样化,固定资产投资对经济贡献程度没有北方地区高。 |
 |
| 通过市场化回归系数图可以看出,市场化进程有利于促进省域经济发展,不过这种促进作用呈现由东部向西部的递减趋势,东部沿海地区影响程度要明显高于其他地区。其主要原因是在市场化改革逐渐深入的过程中,各地区的市场化进程并不同步,东部沿海地区优惠扶持政策推行相对更早,改革力度也较大,而中西部地区相对迟缓。作为驱动经济增长的重要制度性因素,市场化改革无疑会拉大地区间经济发展差距。 |
|
|
-
3)、可选系数栅格表面:
| POP |
INVEST |
INDEX |
|
|
|
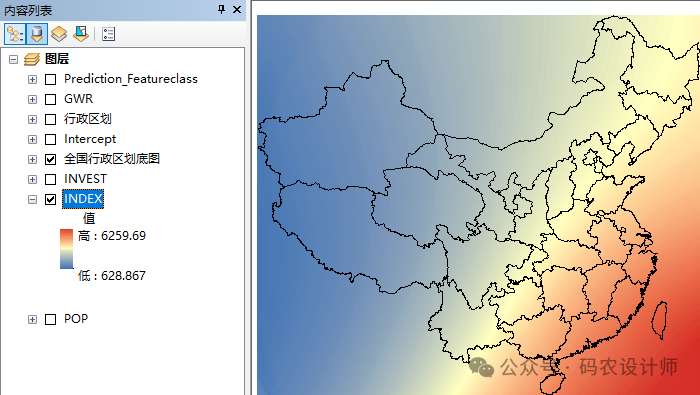 |
-
4)、预测输出要素类:
将 GWR 应用于采样数据时,可使用它进行预测。为因变量未知的位置指定包含所有解释变量的要素类,然后创建具有因变量估计值的新输出要素类。


本篇文章来源于微信公众号: 码农设计师





