本系列配套练习数据下载链接:
链接:https://pan.baidu.com/s/1imKDcw9wZWk_ItR8fwugZw?pwd=mnsj 提取码:mnsj
如有需要请尽快下载。如若失效,我也会在最新发布文章中更新下载链接。
通过叠加分析工具可以将权重应用到多个输入图层中,将它们合并成一个输出,同时遵守分布与形状规范,并标识该结果范围内的首选位置。
叠加分析工具集包括加权叠加、加权总和、模糊隶属度、模糊叠加、查找区域五个工具。
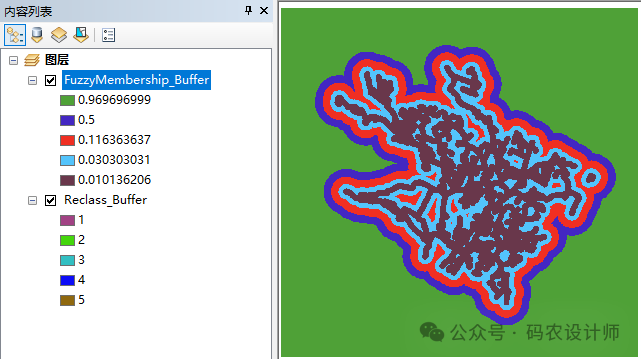
模糊隶属度工具用于根据模糊隶属度函数将输入栅格转换为 0 到 1 之间的范围,指示其对某一集合的隶属度,其中0表示完全不属于该模糊集,1表示完全属于该模糊集。
模糊隶属度工具的原理基于模糊逻辑,这是一种处理不确定性和模糊性的数学方法。
传统逻辑(如布尔逻辑)是二值的,意味着事物要么是真(1),要么是假(0)。这种逻辑在处理明确、精确的问题时非常有效。然而,现实生活中许多问题都是模糊的,难以用简单的真或假来描述。
模糊逻辑则引入了“隶属度”的概念。在模糊逻辑中,一个事物可以部分地属于某个集合,允许事物处于“真”和“假”之间的模糊状态。例如,我们可以说某天的天气“有点热”,这里的“有点”就表示了一种隶属度,即天气属于“热”这个集合的程度。
再比如,我们用传统逻辑来判断一个人是否“高个子”。如果一个人身高超过 180 厘米,那么他就是“高个子”,否则就不是。但是,如果一个人身高 178 厘米,他是否算是“高个子”呢?传统逻辑无法给出明确的答案。而模糊逻辑则可以解决这个问题。我们可以定义一个模糊集合“高个子”,并规定身高 180 厘米以上的人完全属于这个集合,身高 160 厘米以下的人完全不属于这个集合,身高 160 厘米到 180 厘米之间的人部分属于这个集合。这样,我们就可以根据一个人的身高计算他属于“高个子”的程度。
模糊逻辑的优点在于它能够更灵活地处理不精确或不确定性信息,这使得它在很多实际应用中具有很强的优势。
关于模糊逻辑的更多内容可以查看官方文档:
模糊隶属度函数的主要作用就是量化模糊性。比如,对于“热”这个概念,不同的人可能有不同的理解。有些人认为超过25°C就算热,而有些人可能要等到超过30°C才觉得热。模糊隶属度函数就能考虑到这种差异,给出一个介于0和1之间的数值,表示当前温度属于“热”这个概念的程度。
ArcGIS 模糊隶属度工具支持以下几种常见的模糊隶属度函数,将输入栅格值转换为模糊隶属度值:
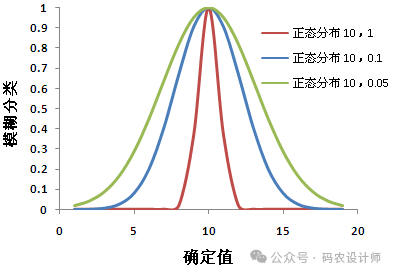
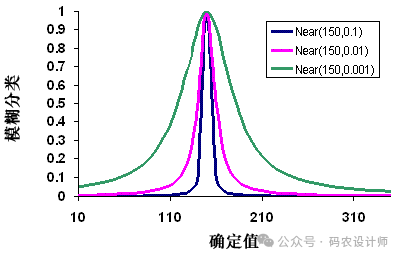
使用高斯(正态)分布的形状来定义输入数据的隶属度。中心值 (μ) 和标准差 (σ) 参数用于控制高斯曲线的形状。
正态分布的中点为集合定义了理想定义,为该中点分配值 1,而分类过程中的其他输入值随着在正方向和负方向上距该中点的距离的递增而逐渐减小。分类过程中输入值随着距中点的距离的递增而逐渐减小,直至到达输入值与理想定义相距甚远且确实超出集合范围的点为止,为此类输入值分配值 0。

高斯函数适用于当数据点的隶属度根据其距离某个中心点的远近而逐渐变化时,即在特定值的附近进行分类时十分有用。例如,在房屋适宜性模型中,为便于采光,朝南(180 度)可能是最理想的构建方位;小于或大于 180 度的方位都不大理想或更可能位于理想适宜性集合之外。
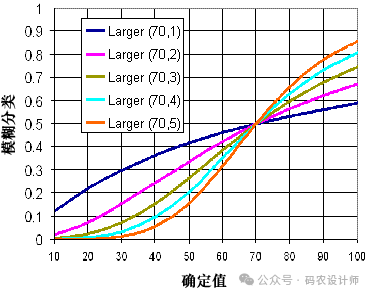
模糊较大值函数根据输入值与最大值的距离,计算模糊隶属度值。值越大,隶属度越高。
当较大的输入值更可能是集合的成员时,将使用模糊较大值变换函数。定义的中点用于确定交叉点(分配的分类为 0.5),大于中点的值成为集合成员的概率较高,小于中点的值成为集合成员的概率较低。展开参数用于定义过渡区的形状和特征。

图片来源:ArcMap官方文档
在需要识别空间数据中的相对高值区域时使用,例如在房屋适应性模型中,模糊较大值函数可用于对垃圾填埋场图层中的距离值进行转换。与垃圾填埋场之间的距离越大,就越可能成为良好适宜性集合中的成员。
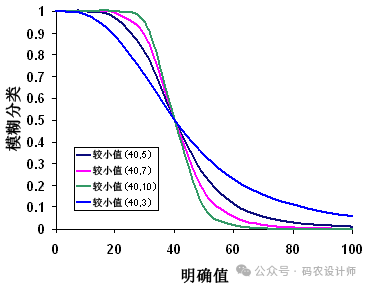
模糊较小值函数根据输入值与最小值的距离,计算模糊隶属度值。值越小,隶属度越高。
当较小的输入值更可能成为集合的成员时,将使用模糊较小值变换函数。定义的中点用于确定交叉点(分配的分类为 0.5),大于中点的值成为集合成员的概率较低,小于中点的值成为集合成员的概率较高。展开参数用于定义过渡区的形状和特征。

图片来源:ArcMap官方文档
在寻找空间数据中的相对低值区域时使用,例如房屋适宜性示例中的模糊较小值变换函数可用于表示与供电条件之间的距离。随着与电力线之间的距离不断增大,获取供电的费用将逐渐升高,因此,这些区域成为良好适宜集合成员的概率将逐渐减小。
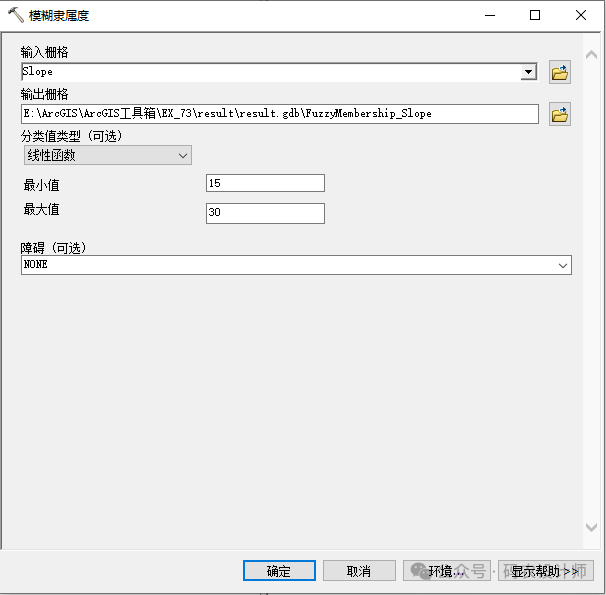
该函数允许用户对输入数据进行线性变换,以改变其隶属度值的范围和分布。
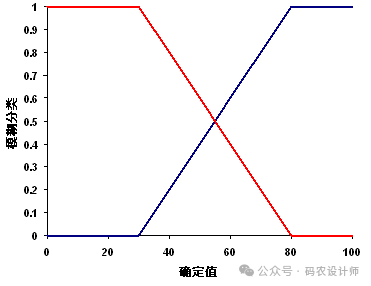
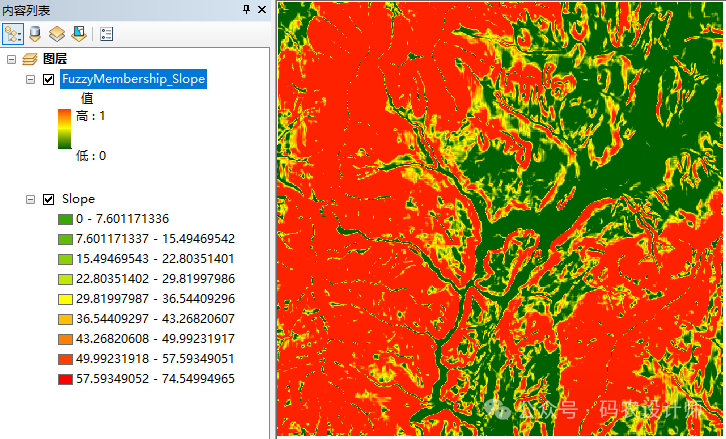
将在用户指定的最小值和最大值之间应用线性函数。低于最小值的所有值够将分配为 0(确定不是成员),高于最大值的所有值都将分配为 1(确定是成员)。下图中的蓝线表示正坡度线性变换,其中最小值为 30,最大值为 80。低于 30 的所有值都分配为 0,高于 80 的所有值都分配为 1。
如果最小值大于最大值,则建立负线性关系(负坡度)。下图中的红线表示负坡度线性变换。低于 30 的任何值都将分配为 1,高于 80 的任何值都将分配为 0。

图片来源:ArcMap官方文档
在需要对原始数据进行缩放、平移或其他线性调整时使用,以适应特定的分析或显示需求。例如,房屋适宜性示例中的模糊线性变换函数可用于表示与娱乐区条件之间的距离(负线性变换)。位于娱乐区 500 米范围之内的任何位置可能确定位于良好的适宜集合内;在 500 到 10,000 米之间,属于适宜集合的概率呈线性递减;10,000 米以外的任何位置因距娱乐区的距离过远而无法成为适宜集合的一部分,并将被分配值 0。
模糊 MS 较大值变换函数与模糊较大值函数相似,只不过该函数是基于指定的平均值和标准差来定义的。通常,这两个函数之间的差别在于:如果极大值更可能成为集合的成员,则采用模糊 MS 较大值函数可能更加适合。函数会根据输入数据的均值和标准差来计算每个数据点的隶属度,突出显示那些相对较大的值。
结果可能与模糊较大值函数相似,具体取决于定义的平均值和标准差。
模糊 MS 较小值变换函数与模糊较小值函数相似,只不过该函数是基于指定的平均值和标准差来定义的。通常,这两个函数之间的差别在于:如果极小值更可能成为集合的成员,则采用模糊 MS 较小值函数可能更加适合。
结果可能与模糊较小值函数类似,具体取决于定义的平均值和标准差。
该函数用于评估输入数据点相对于某个指定值或范围的接近程度。
如果在特定值附近进行分类,则最适合采用模糊邻近值变换函数。该函数由定义集合中心的中点定义,该中点可确定明确的成员并因此分配为值 1。随着值从中点开始在正方向和负方向上移动,分类将递减至 0(不定义分类)。展开参数用于定义过渡区的宽度和特征。
模糊邻近值和模糊高斯可能比较相似,具体取决于指定的参数。与模糊高斯函数相比,模糊邻近值函数通常以更快的速率递减,展开幅度也更窄;因此,当紧邻中点的值更可能成为集合的成员时,将使用此函数。

在使用时,需要根据输入栅格数据的类型和应用场景选择合适的模糊隶属度函数。
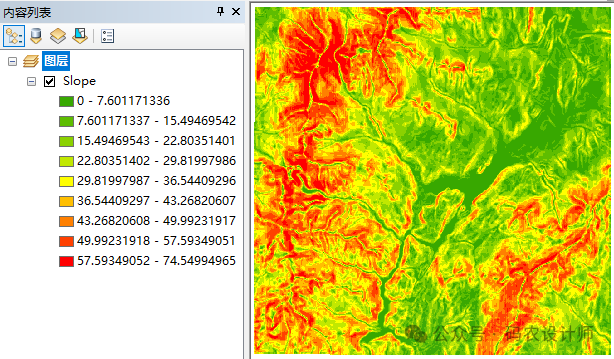
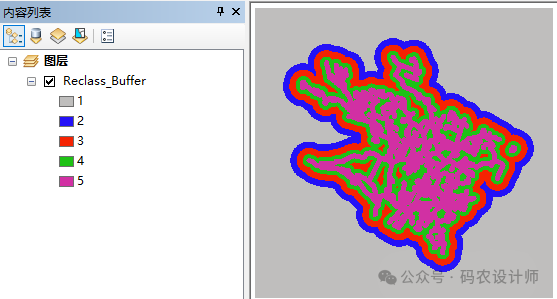
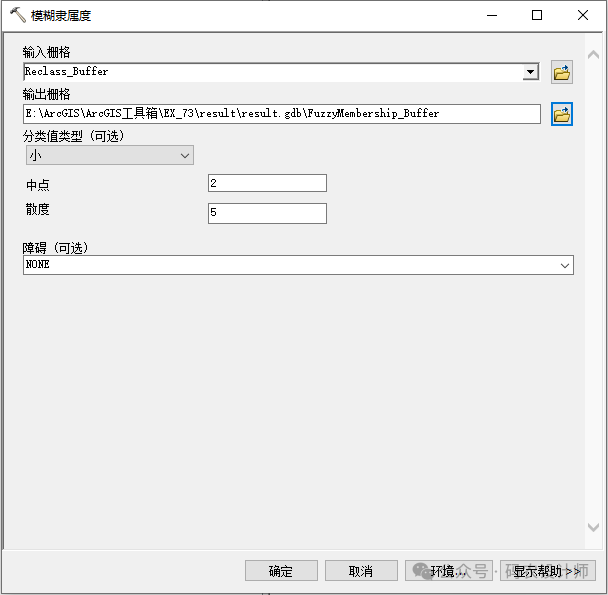
加载坡度数据【Slope】、坡向数据【Aspect】以及重分类后的距离栅格数据【Reclass_Buffer】。
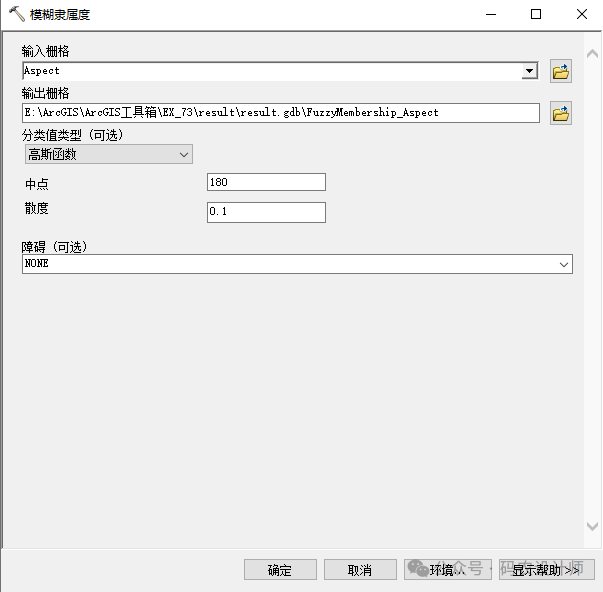
选择【系统工具箱→Spatial Analysis Tools→叠加分析→加权叠加】工具,在弹出的对话框中进行设置。主要是根据数据类型和应用场景选择合适的模糊隶属度函数,并设置相应的参数值。









————————————————-
《ArcGIS工具箱》系列内容目录(持续更新):

本篇文章来源于微信公众号: 码农设计师