本系列文章是根据Shapely官方文档翻译整理,学习任何一个Python第三方库,其官方文档都是最好的学习资料。相比网络搜索得到的一些资料,官方文档是权威的一手资料,其内容全面、准确可靠。通过官方文档入手,能够保证学习认知不会有大偏差。在学习完官方文档后,可以在寻找其他资料进一步学习。
点击“阅读原文”或者直接访问下方链接,查看翻译整理的“Shapely 2.0.0 中文文档”。
https://www.mizhushare.com/docs/shapely-2-0-0-%e4%b8%ad%e6%96%87%e6%96%87%e6%a1%a3/-
可以通过百度网盘获取,需要在本地配置代码运行环境:
链接:https://pan.baidu.com/s/1iWGGhB4kra9V7bUj-CWR0w?pwd=mnsj提取码:mnsj
-
前往GitHub详情页面,单击 code 按钮,选择Download ZIP选项:
https://github.com/returu/Shapely1.子集:
-
shapely.ops.substring(geom,start_dist,end_dist,normalized=False):
返回start_dist和end_dist之间的LineString,如果它们在同一位置,则返回一个Point。
负的距离值被视为从几何体的末端反向测量,超出范围的索引值是通过将其夹在有效的数值范围内来处理。
如果开始距离实际上超过了结束距离,那么将返回反转的子串,这样开始距离就在第一个坐标上。
如果normalized参数是True,那么距离将被解释为几何体长度的一小部分。
例如:
1>>> from shapely.ops import substring
2
3>>> ls = LineString((i, 0) for i in range(6))
4>>> ls
5<LINESTRING (0 0, 1 0, 2 0, 3 0, 4 0, 5 0)>
6
7>>> re1 = substring(ls , start_dist=1 , end_dist=3)
8>>> re1
9<LINESTRING (1 0, 2 0, 3 0)>
10
11>>> re2 = substring(ls , start_dist=3 , end_dist=1)
12>>> re2
13<LINESTRING (3 0, 2 0, 1 0)>
14
15>>> re3 = substring(ls , start_dist=1 , end_dist=-3)
16>>> re3
17<LINESTRING (1 0, 2 0)>
18
19>>> re4 = substring(ls , start_dist=0.2 , end_dist=-0.6 , normalized=True)
20>>> re4
21<LINESTRING (1 0, 2 0)>
结果如图所示:


2.制备几何操作:
Shapely几何对象可以被加工成一种 可以支持高效批量操作的形式,称为制备几何操作。
-
prepared.prep(ob):
例如,检测大量点中有哪些落入多边形(灰色)中,作为示例,只设置了5个点(红色):
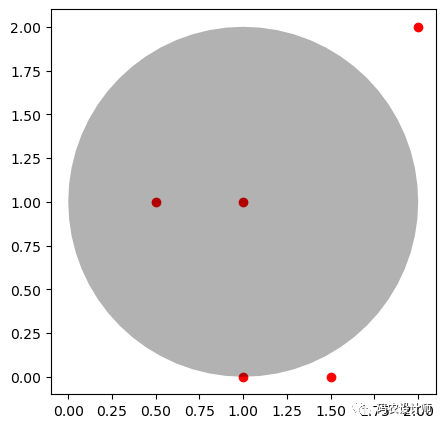
1>>> from shapely.prepared import prep
2
3>>> points = [Point(1, 1) , Point(2, 2) , Point(1, 0), Point(0.5, 1), Point(1.5, 0)] # large list of points
4>>> points
5[<POINT (1 1)>, <POINT (2 2)>, <POINT (1 0)>, <POINT (0.5 1)>, <POINT (1.5 0)>]
6
7>>> polygon = Point(1, 1).buffer(1.0)
8>>> polygon
9<POLYGON ((2 1, 1.995 0.902, 1.981 0.805, 1.957 0.71, 1.924 0.617, 1.882 0.5...>
10
11# prepared.prep(ob)函数创建并返回制备几何对象
12>>> prepared_polygon = prep(polygon)
13>>> prepared_polygon
14<shapely.prepared.PreparedGeometry object at 0x0000019467B394F0>
15
16# 使用contains函数检测点是否在多边形内部
17# 再使用filter函数过滤序列,返回符合条件的元素组成的新列表
18>>> hits = filter(prepared_polygon.contains, points)
19>>> hits
20<filter object at 0x0000019467B390D0>
21
22>>> for x in hits:
23... print(x.wkt)
24...
25POINT (1 1)
26POINT (0.5 1)
制备几何对象实例有以下方法:contains, contains_properly, covers, intersects。所有这些方法的参数和用法都与非制备几何对象中的对应方法完全相同。
3.极点:
-
shapely.ops.polylabel(polygon, tolerance):
Vladimir Agafonkin的polylabel。1>>> from shapely.ops import polylabel
2
3>>> polygon = LineString([(0, 0), (50, 200), (100, 100), (20, 50),(-100, -20), (-150, -200)]).buffer(100)
4>>> polygon
5<POLYGON ((-75.573 110.02, -47.014 224.254, -44.199 233.565, -40.492 242.559...>
6
7>>> label = polylabel(polygon , tolerance=10)
8>>> label
9<POINT (59.356 121.839)>
多边形的极点与中心点位置关系如下图所示:


END

本篇文章来源于微信公众号: 码农设计师
