本系列文章是根据Shapely官方文档翻译整理,学习任何一个Python第三方库,其官方文档都是最好的学习资料。相比网络搜索得到的一些资料,官方文档是权威的一手资料,其内容全面、准确可靠。通过官方文档入手,能够保证学习认知不会有大偏差。在学习完官方文档后,可以在寻找其他资料进一步学习。
点击“阅读原文”或者直接访问下方链接,查看翻译整理的“Shapely 2.0.0 中文文档”。
https://www.mizhushare.com/docs/shapely-2-0-0-%e4%b8%ad%e6%96%87%e6%96%87%e6%a1%a3/-
可以通过百度网盘获取,需要在本地配置代码运行环境:
链接:https://pan.baidu.com/s/1iWGGhB4kra9V7bUj-CWR0w?pwd=mnsj提取码:mnsj
-
前往GitHub详情页面,单击 code 按钮,选择Download ZIP选项:
https://github.com/returu/Shapelyclass Point(coordinates):Point构造函数接受位置坐标值或点的元组参数。
1# 传入两个参数:点的x,y坐标
2>>> point = Point(0.0, 0.0)
3>>> point
4<POINT (0 0)>
5
6# 传入点的x,y坐标值组成的元祖
7>>> Point((0.0, 0.0))
8<POINT (0 0)>
9
10# 传入三个参数:点的x,y坐标以及代表高程信息的z值
11>>> Point(1,1,2)
12<POINT Z (1 1 2)>
area、length属性:点的面积、长度均为零。
1>>> point.area , point.length
2(0.0, 0.0)
bounds属性:点的x-y边界是一个(minx, miny, maxx, maxy)元组,边界坐标就是点本身的坐标值。
1>>> point.bounds
2(0.0, 0.0, 0.0, 0.0)
点的坐标值通过coords、x、y和z属性访问。
1>>> list(point.coords)
2[(0.0, 0.0)]
3
4>>> point.x , point.y
5(0.0, 0.0)
6
7>>> list(Point(1,1,2).coords)
8[(1.0, 1.0, 2.0)]
9
10>>> Point(1,1,2).x , Point(1,1,2).y , Point(1,1,2).z
11(1.0, 1.0, 2.0)
coords属性也支持切片操作。
1>>> point.coords[:]
2[(0.0, 0.0)]
3
4>>> point.coords[0]
5(0.0, 0.0)
点的构造函数也接受另一个点的实例,从而产生一个副本。
1>>> Point(point)
2<POINT (0 0)>
3
4# 查看几何对象的几何类型
5>>> Point(point).geom_type
6'Point'
class LineString(coordinates) :LineString构造函数接收2个或多个(x, y[, z])点元祖。
1>>> line = LineString([(0,0),(1,1),(2,1)])
2>>> line
3<LINESTRING (0 0, 1 1, 2 1)>
构建的LineString对象代表一个或多个点之间的连接线性样条。允许在有序序列中有重复的点,但可能会产生性能惩罚,因此应当避免。一个LineString对象可以与自己交叉(即复杂几何对象而非简单几何对象)。
在Shapely中,线状几何要素分为简单线(下图a)和复杂线(下图b,复杂线是自相交的)。
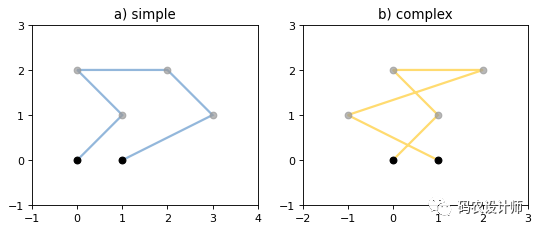
area、length属性:线的面积为零,长度不为零。
1>>> line.area , line.length
2(0.0, 2.414213562373095)
bounds属性:线的x-y边界是一个(minx, miny, maxx, maxy)元组。
1>>> line.bounds
2(0.0, 0.0, 2.0, 1.0)
线对象定义的坐标值可以通过coords属性访问。
1>>> len(line.coords)
23
3
4>>> list(line.coords)
5[(0.0, 0.0), (1.0, 1.0), (2.0, 1.0)]
coords属性支持切片操作。
1>>> line.coords[:]
2[(0.0, 0.0), (1.0, 1.0), (2.0, 1.0)]
3
4>>> line.coords[0]
5(0.0, 0.0)
线构造函数也接收另一个LineString实例,从而得到一个副本。
1>>> LineString(line)
2<LINESTRING (0 0, 1 1, 2 1)>
LineString也可以使用混合点实例或坐标元祖来构造。各个坐标值会被复制到新的对象中。
1>>> LineString([Point(0,0) , (1,1) , Point(2,3)])
2<LINESTRING (0 0, 1 1, 2 3)>
class LinearRing(coordinates) :LinearRing构造函数接收一个有序序列(x, y[, z])的点元祖。
1>>> ring = LinearRing([(0,0) , (1,1) , (1,0)])
2>>> ring
3<LINEARRING (0 0, 1 1, 1 0, 0 0)>
传递的有序序列通过在第一个和最后一个点传递相同的值来明确地闭合线环。否则,会将第一个点复制到最后一个点来隐式闭合线环。与LineString一样,允许有序序列中重复点,但可能会产生性能损失,应该避免。LinearRing不能与自己自相交,也不能在一个单点上接触。
下图a为有效线环,下图b为无效线环(需要注意的是,Shapely不会阻止这种环的创建,但是当它们被操作时,可能会出现异常。)。
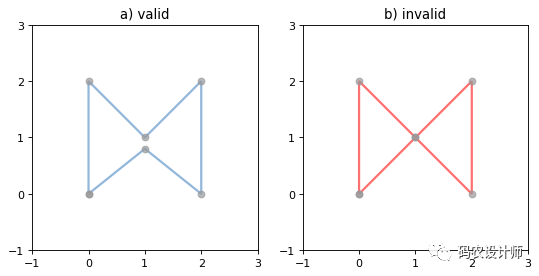
area、length属性:一个LinearRing的面积为零,长度不为零。
1>>> ring.area , ring.length
2(0.0, 3.414213562373095)
bounds属性:一个LinearRing的边界是一个元组(minx, miny, maxx, maxy)。
1>>> ring.bounds
2(0.0, 0.0, 1.0, 1.0)
定义的坐标值可以通过coords属性访问的。
1>>> ring.coords
2<shapely.coords.CoordinateSequence object at 0x000002756A0E0CD0>
3
4>>> len(ring.coords)
54
6
7>>> list(ring.coords)
8[(0.0, 0.0), (1.0, 1.0), (1.0, 0.0), (0.0, 0.0)]
LinearRing构造函数也接收另一个LineString或LinearRing实例,从而得到一个副本。
1>>> LinearRing(ring)
2<LINEARRING (0 0, 1 1, 1 0, 0 0)>
与LineString一样,可以使用混合点实例或坐标元祖来构造。
1>>> LinearRing([Point(0,0) , (1,1) , Point(1,0)])
2<LINEARRING (0 0, 1 1, 1 0, 0 0)>

END

本篇文章来源于微信公众号: 码农设计师
